To be continued

Quantum Neural Networks

1. Basic idea of QNN
   • Architecture of QNN
   • Training QNN
2. Barren Plateaus in QNN
3. QCNN
4. DQNN

• Basic idea of QNN
  • Architecture of QNN
    • 1.data input
    • 2 neural network
    • 3 cost function
    • 4 gradient descent
  • Training QNN
• Barren plateaus in QNN
• QCNN
• Reference
• Appendix

1.1. Basic idea of QNN

1.1.1. Architecture of QNN

We introduce architecture of QNN by comparing it with the classical artificial neural network

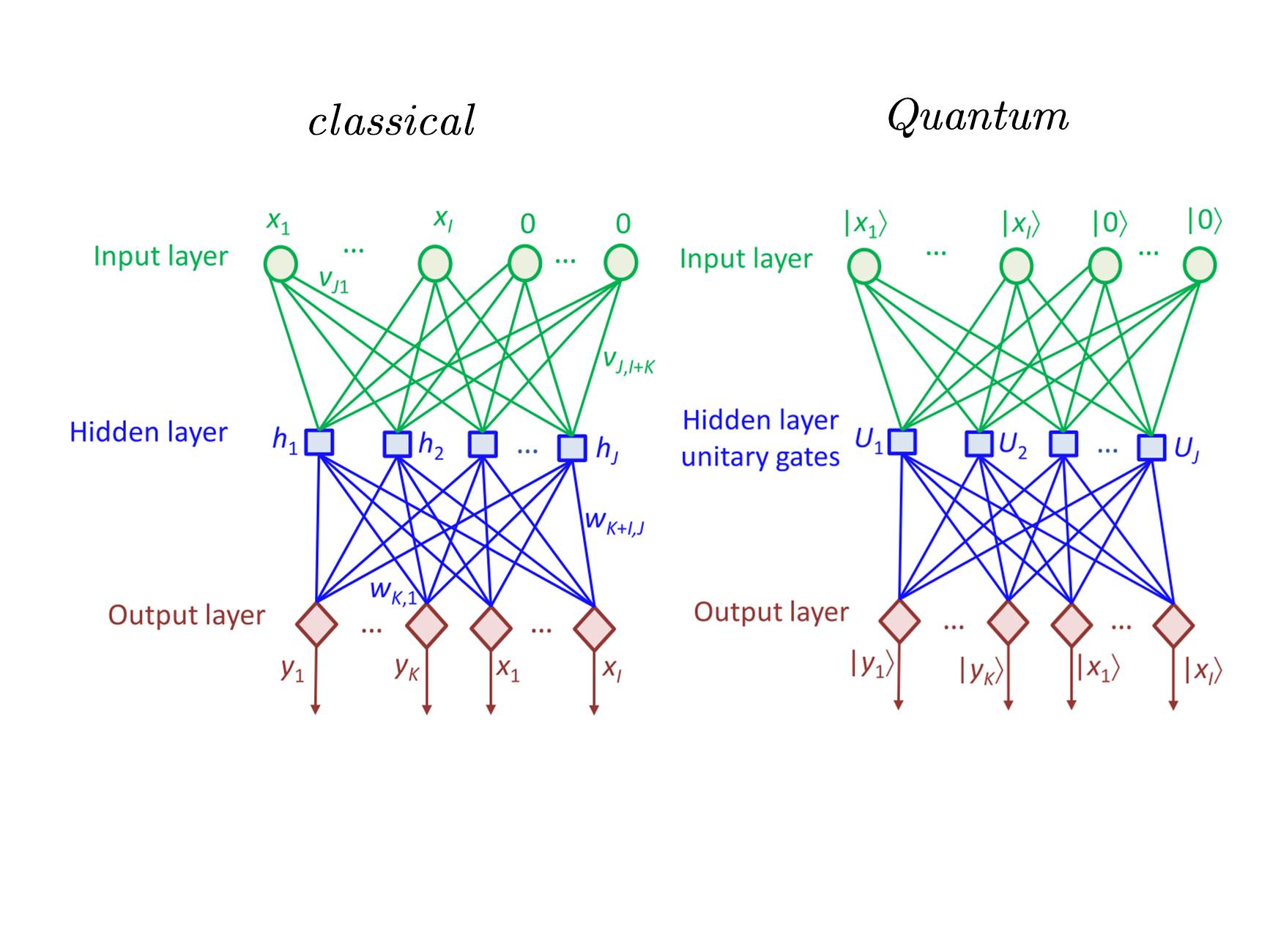
1.data input

$\begin{aligned} x_i=\left[x_{i, 0}, \ldots, x_{i, L-1}\right]^T \\ \Downarrow \\ \left|x_i\right\rangle=\left|x_{i, 0}\right\rangle \otimes \ldots \otimes\left|x_{i, L-1}\right\rangle \end{aligned}$

2 neural network

neural network $\longrightarrow$ unitary quantum gates $U_{j}(j=1, \ldots, J)$

The action of the $j$ th unitary operator on $M=I+K$ qubits can be represented by: $U_{i}=\exp \left[j \sum_{m_{1}, \ldots, m_{M}=0 \ldots 0}^{3 \ldots 3} \alpha_{m_{1}, \ldots, m_{N}}^{(i)} \sigma_{m_{1}}^{(i)} \otimes \ldots \otimes \sigma_{m_{N}}^{(i)}\right]$ where

• $\sigma_{m_{l}} \in\{I, X, Y, Z\}$ represent the Pauli matrices.

3 cost function

$C=-\sum_{n=1}^{N}\left\langle y _{U}^{(n)} \mid y ^{(n)}\right\rangle$

where

• $y _{U}^{(n)}$ is dependent on the unitary operator parameters $\alpha_{m_{1}, \ldots, m_{N}}^{(i)}$
• $y ^{(n)}$ represents the labels at the output neurons for the $n$th training instance $(n=1, \ldots, N)$.

4 gradient descent

We can use the gradient descent to update the $\alpha$ parameters in the $i$ th unitary matrix as follows: $\Delta \alpha_{m_{1}, \ldots, m_{N}}^{(i)}=-\eta \frac{\partial C}{\partial \alpha_{m_{1}, \ldots, m_{N}}^{(i)}}$

$\Delta \alpha_{m_{1}, \ldots, m_{N}}^{(i)}=-\eta \frac{\partial C}{\partial \alpha_{m_{1}, \ldots, m_{N}}^{(i)}}$

1.1.2. Training QNN

1. Ricks, Bob, and Dan Ventura. "Training a quantum neural network." Advances in neural information processing systems 16 (2003).
2. Beer, Kerstin, et al. "Training deep quantum neural networks." Nature communications 11.1 (2020): 1-6.
3. Zhang, Kaining, et al. "Toward trainability of deep quantum neural networks." arXiv:2112.15002 (2021).

To be continued

1.2. Barren plateaus in QNN

1. arXiv:1803.11173 (2018) Barren plateaus in quantum neural network training landscapes

Exponential decay of variance.

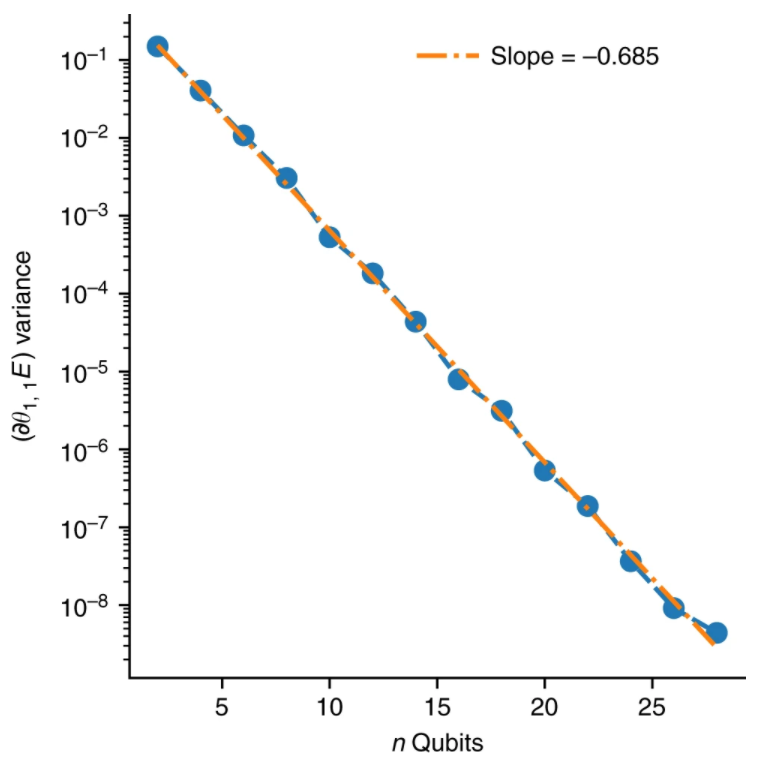
The sample variance of the gradient of the energy for the first circuit component of a two-local Pauli term $\left(\partial_{\theta_{1}, 1} E\right)$ plotted as a function of the number of qubits on a semi-log plot. As predicted, an exponential decay is observed as a function of the number of qubits, $n$, for both the expected value and its spread. The slope of the fit line is indicative of the rate of exponential decay as determined by the operator

variance of measurements $\operatorname{Var}\left[\partial_{k} E\right] \approx\left\{\begin{array}{l} -\frac{\operatorname{Tr}\left(\rho^{2}\right)}{\left(2^{2 n}-1\right)} \operatorname{Tr}\left\langle\left[V, u^{\dagger} H u\right]^{2}\right\rangle_{U_{+}} \\ -\frac{\operatorname{Tr}\left(H^{2}\right)}{\left(2^{2 n}-1\right)} \operatorname{Tr}\left\langle\left[V, u \rho u^{\dagger}\right]^{2}\right\rangle_{U_{-}} \\ \frac{1}{2^{(3 n-1)}} \operatorname{Tr}\left(H^{2}\right) \operatorname{Tr}\left(\rho^{2}\right) \operatorname{Tr}\left(V^{2}\right) \end{array}\right.$ where The average value of the gradient $\left\langle\partial_{k} E\right\rangle=\int d U p(U) \partial_{k}\left\langle 0\left|U( \theta )^{\dagger} H U( \theta )\right| 0\right\rangle$ where the gradient of the objective function $\partial_{k} E \equiv \frac{\partial E( \theta )}{\partial \theta_{k}}=i\left\langle 0\left|U_{-}^{\dagger}\left[V_{k}, U_{+}^{\dagger} H U_{+}\right] U_{-}\right| 0\right\rangle$

1.3. QCNN

Absence of Barren Plateaus in Quantum Convolutional Neural Networks

1.4. Reference

What is QNN

1. A review of Quantum Neural Networks: Methods, Models, Dilemma arXiv:2109.01840
2. Kak, S. (1995). "On quantum neural computing". Advances in Imaging and Electron Physics. 94: 259–313. doi):10.1016/S1076-5670(08)70147-270147-2)
3. Efficient Learning for Deep Quantum Neural Networks (2020) arXiv:1902.10445
   • Training deep quantum neural networks Nat Commun 11, 808 (2020)
4. On quantum neural networks 2021 arXiv:2104.07106
   • early definition of QNN & modern definition of QNN

What problem QNN advantage in?

1. The Power of Quantum Neural Networks 2020 arXiv:2011.00027
2. Power of data in quantum machine learning 2021 arXiv:2011.01938

What is （Barren Plateau）in QNN ?

1. Barren plateaus in quantum neural network training landscapes
2. Cost function dependent barren plateaus in shallow parametrized quantum circuits Nature Communications 12, 1791 (2021)
3. Trainability of Dissipative Perceptron-Based Quantum Neural Networks arxiv.2005.12458

What make（Barren Plateau）?

1. explain
2. arXiv: 2010.15968 Entanglement Induced Barren Plateaus

What is QCNN

2019 Harve

• Nature Physics 15,1273-1278(2019) Quantum convolutional neural networks
• A Tutorial on Quantum Convolutional Neural Networks (QCNN) arxiv.2009.09423
• TensorFlow implements QCNN

absence Barren Plateau in QCNN

1. Absence of Barren Plateaus in Quantum Convolutional Neural Networks

1.5. Appendix