To be continued

Variational Algorithms

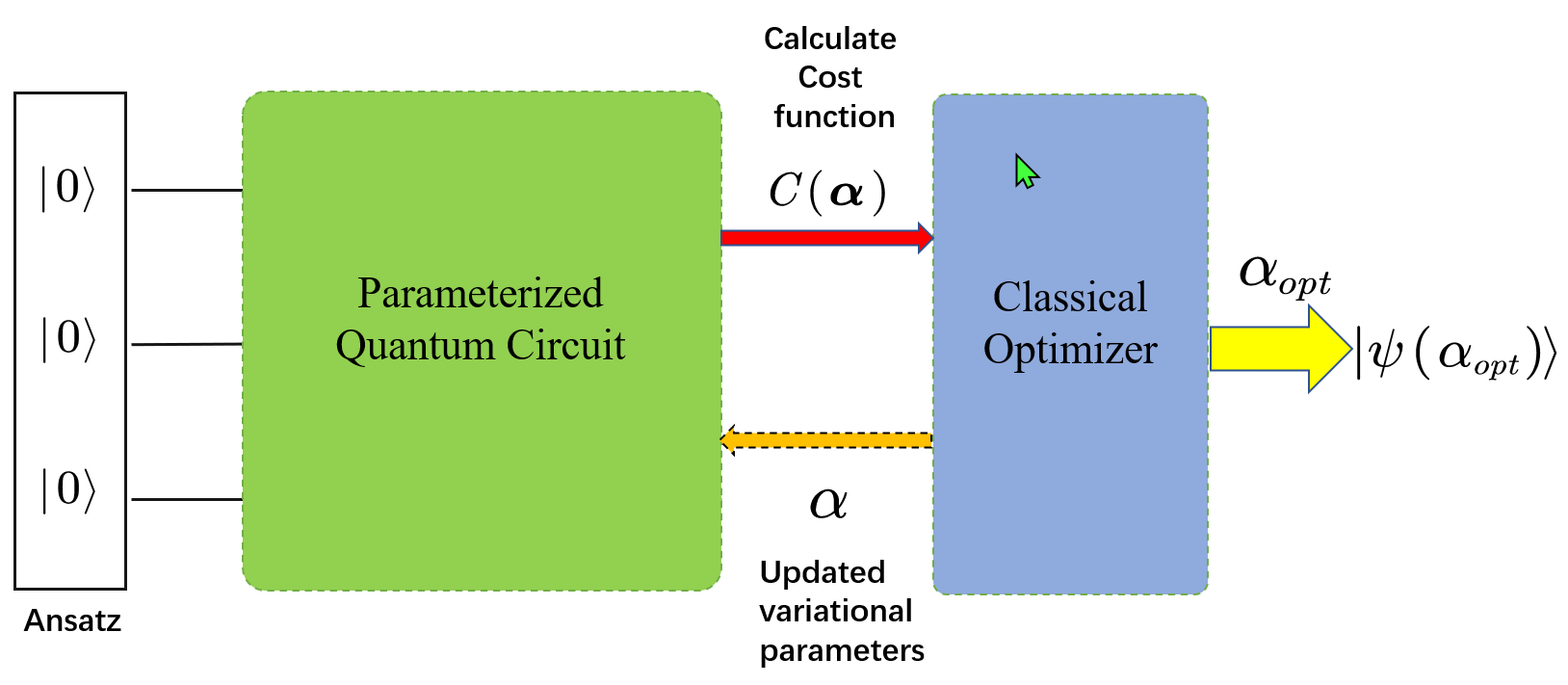
1. Basic idea
2. Building block
   • Cost function
   • Ansatzes
   • Optimizers

• Reference
  • Review
  • Barren plateaus
  • others
• Basic idea

1. Reference

1.1.1. Review

1. Cerezo, Marco, et al. "Variational quantum algorithms." Nature Reviews Physics 3.9 (2021): 625-644. arXiv:2012.09265
2. McClean, Jarrod R., et al. "The theory of variational hybrid quantum-classical algorithms." New Journal of Physics 18.2 (2016): 023023. arXiv:1509.04279

1.1.2. Barren plateaus

1. McClean, Jarrod R., et al. "Barren plateaus in quantum neural network training landscapes." Nature communications 9.1 (2018): 1-6. arXiv:1803.11173
2. Marrero, Carlos Ortiz, Mária Kieferová, and Nathan Wiebe. "Entanglement-induced barren plateaus." PRX Quantum 2.4 (2021): 040316. arXiv:2010.15968
3. Wang, Samson, et al. "Noise-induced barren plateaus in variational quantum algorithms." Nature communications 12.1 (2021): 1-11. arXiv:2007.14384

1.1.3. others

1. Bittel, Lennart, and Martin Kliesch. "Training variational quantum algorithms is np-hard." Physical Review Letters 127.12 (2021): 120502. arXiv:2101.07267
2. Lyu, Chufan, et al. "Symmetry enhanced variational quantum eigensolver." (2022). arXiv:2203.02444

2. Basic idea

1. The cost function you select depends on your task
2. Design short-depth quantum circuit to calculate your cost function
3. Parameterized gate sequence to formulate Ansatz
4. Choose a classical optimizer to design the training algorithm

To be continued