Topological quantum computation

• Anyon models
  • Fusion rules ~ state and fusion channel
    • Fusion diagrams ~ $f-$-matrices">$F-$ matrices ~ $r-$-matrices">$R-$ matrices
  • Example 1: Fibonacci anyons
  • Example 2: Ising anyons
• Quantum computation with anyons
  • Elementary braiding
  • Braiding to Gate
  • Braid Implementation of Algorithm
• Appendix
  • Knot Invariant of the Jones polynomial

Reference

1. 《A Short Introduction to Topological Quantum Computation》 (2017) V.T. Lahtinen, J.K. Pachos
2. 《Introduction to topological quantum computation with non-Abelian anyons》 (2018) Bernard Field and Tapio Simula
3. 《Introduction To Topological Quantum Computation》Pachos, Jiannis K.
4. 《Quantum Computation with Topological Codes From Qubit to Topological Fault-Tolerance》 Keisuke Fujii

In the field of topological phase matter, Majorana zero modes(MZM) is one of the concerns of physicists, because MZM has the potential to construct topological quantum computing. Topological quantum computation(TQC) is an approach to storing and manipulating quantum information that employs exotic quasiparticles, called anyons. Majorana zero modes behave like a special kind of anyons called ising anyons.

In this chapter, we will introduce Anyon models, include Fusion channels and braiding anyons. Two examples will be shown, include Fibonacci anyons and Ising anyons. Then we will introduce the quantum computation with anyons. From initialization, to quantum gates and measurements.

1. Anyon models

We first ignore the issue of the physical implementation of anyons, assume that anyons exist and then focus on explaining the types and corresponding properties of anyons.

Two types of anyons as examples

1. Fibonacci anyons
2. Ising anyons

Three simple properties of anyons

1. Anyons can be created or annihilated in pairwise fashion.
2. Anyons can be fused to form other types of anyons.
3. Anyons can be exchanged adiabatically.

In the following, we describe these properties in mathematical language.

1.1. Fusion rules

The anyon model is spanned by some number of particles $M=\{1, a, b, c, \ldots\}$ where

• a trivial label, 1, corresponding to the vacuum with no anyons.
• the labels $a, b, c, \ldots$ can be viewed as topological charges carried by each anyon.

charges conservation rules in anyons are known as fusion rules $a \times b=\sum_{c \in M} N_{a b}^c c,$ where

• the fusion coefficients $N_{a b}^c=0,1, \ldots$ are non-negative integers describing the possible fusion channels
• non-Abelian anyons always have multiple fusion channels $\sum_c N_{a b}^c>1$

state and fusion channel

The fusion channel degrees of freedom of non-Abelian anyons imply a space of states spanned by different possible fusion outcomes.

For example, if $a$ and $b$ can fuse to several $c \in M$, we can define orthonormal states $|a b ; c\rangle$ that satisfy $\langle a b ; c \mid a b ; d\rangle=\delta_{c d} .$

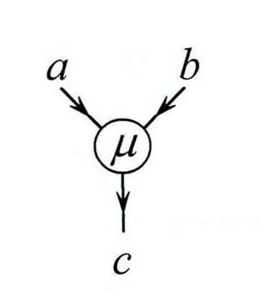
1.1.1. Fusion diagrams

• Anyons $a$ and $b$ are fused into Anyon $c$ throught channel $\mu$
  • state of system $\left|(a b)_c^\mu\right\rangle$

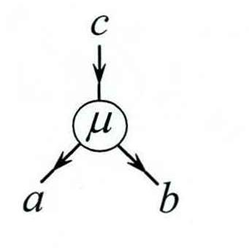
• Conjugate process: Anyon $c$ separate into Anyons $a$ and $b$ throught channel $\mu$
  • state of system $\left\langle(a b)_c^\mu\right|$

$F-$ matrices

For a Anyon model with three Anyons $M=\{a, b, c\}$

• There are the two possible fusion for This model (Two Bases)
• we can define two orthonormal states
  • $\left|\left((a b)_d^\mu c\right)_e^v\right\rangle$
  • $\left|\left(a(b c)_f^\alpha\right)_e^\beta\right\rangle$

For every anyon model, there exists a set of matrices that relate a state in one basis to states in other bases. These matrices are called $F$-matrices. $\left|\left((a b)_d^\mu c\right)_e^v\right\rangle=\sum_{f, \alpha, \beta}\left(F_e^{a b c}\right)_{d \mu v}^{f \alpha \beta}\left|\left(a(b c)_f^\alpha\right)_e^\beta\right\rangle$ Diagrams for the two orthonormal states and $F$-matrices relation between them.

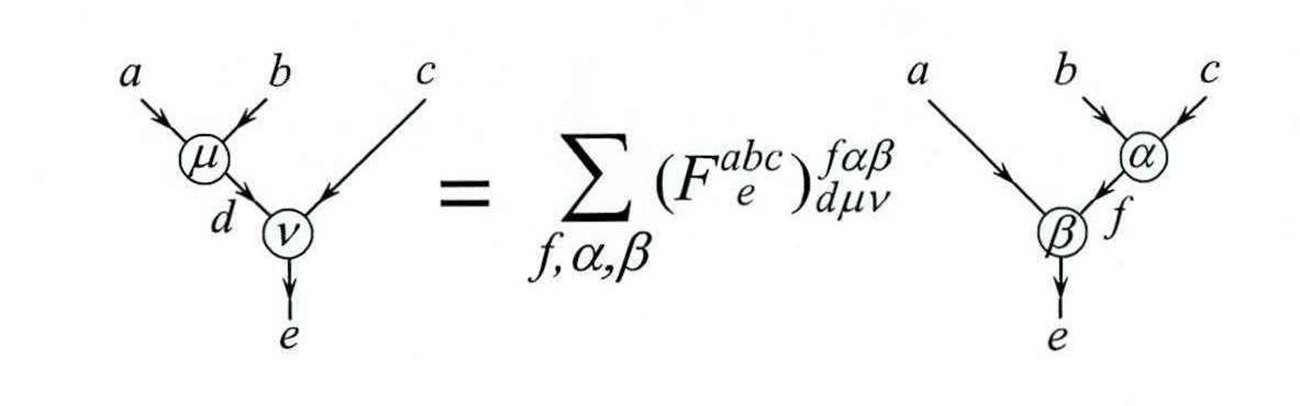
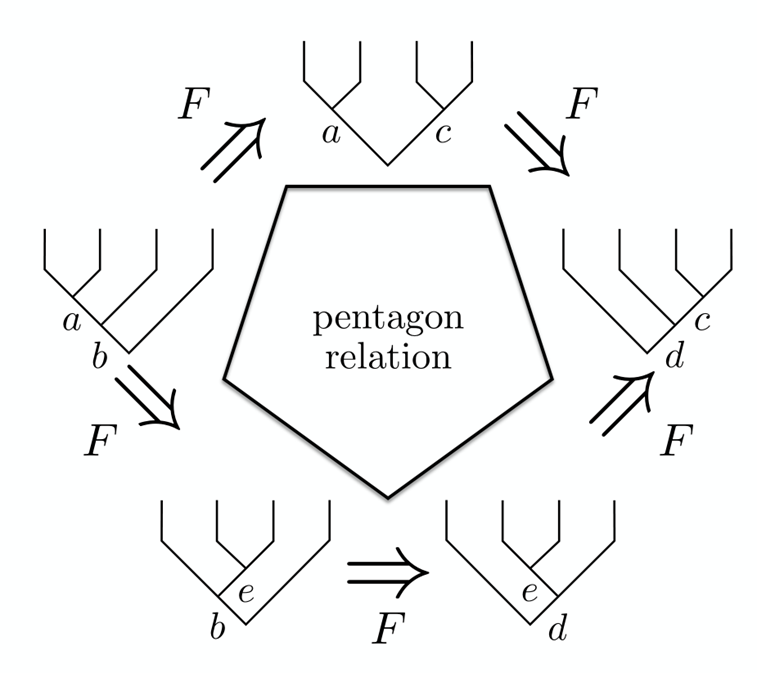
To find the values of $F$-matrices coefficients requires solving a consistency relationship known as the pentagon relationship. $\sum_{\mu_7}\left(F_e^{f c d}\right)_{g \mu_2 \mu_3}^{h \mu_4 \mu_7}\left(F_e^{a b h}\right)_{f \mu_1 \mu_7}^{i \mu_2 \mu_6}=\sum_{j \mu_8 \mu_9 \mu_{10}}\left(F_g^{a b c}\right)_{f \mu_1 \mu_2}^{j \mu_8 \mu_9}\left(F_e^{a j d}\right)_{g \mu_9 \mu_3}^{i \mu_1 \mu_6}\left(F_i^{b c d}\right)_{j \mu_8 \mu_{10}}^{h \mu_4 \mu_5}$ Pentagon equations are not discussed explicitly here

To find the effect of braiding, it is also necessary to consider the effect of exchanging two particles. This is quantified using the $\mathrm{R}$ move,

$R-$ matrices

The effect of exchanging two particles are quantified using the $\mathrm{R}$ matrices.

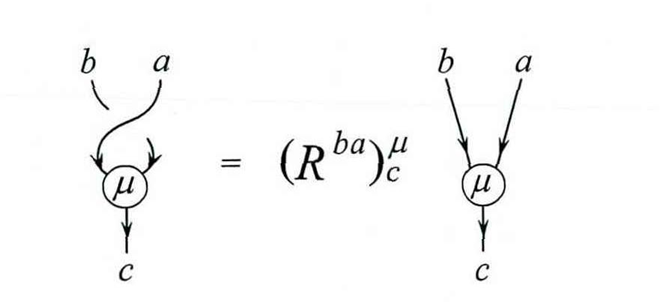
The $R$-matrices coefficients can be found using a consistency relation known as the hexagon relationship $\left(R^{d c}\right)_e^{\mu_2}=\sum_{f \mu_3 \mu_4 g \mu_5 \mu_6}\left(F_e^{b a c}\right)_{d \mu_1 \mu_2}^{f \mu_3 \mu_4}\left(R^{a c}\right)_f^{\mu_3}\left(F_e^{a c b}\right)_{g \mu_3 \mu_4}^{g \mu_4 \mu_6}\left(R^{b c}\right)_g^{\mu_5}\left(F_e^{c b a}\right)_{g \mu_5 \mu_6}^{d \mu_1 \mu_2}$

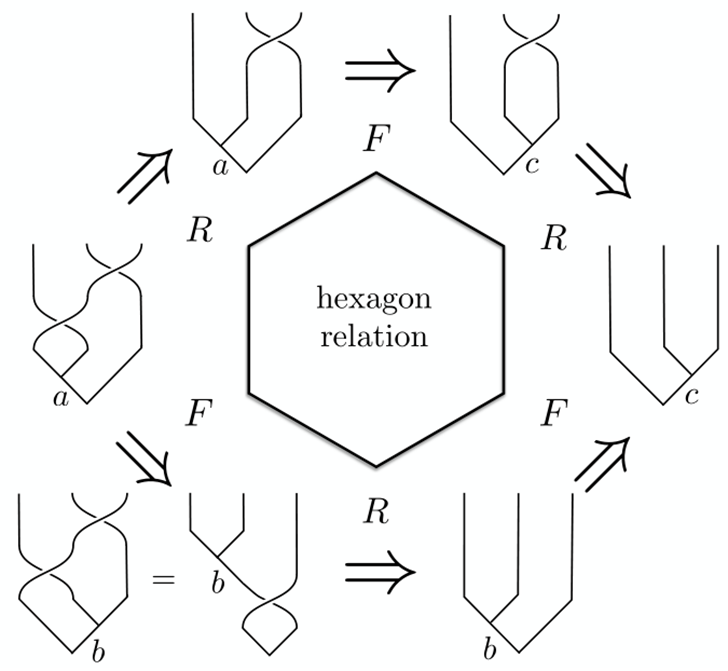
Explicit matrix representations for the effect of braiding can be constructed by performing $F$ and $R$-matrices acting on an appropriate basis state (Preskill, 2004).

1.2. Example 1: Fibonacci anyons

For Fibonacci Anyon model with only two Anyons

• 0
• 1

Fusion rules $\begin{aligned} &0 \times 0=0 \\ &0 \times 1=1 \times 0=0 \\ &1 \times 1=0+1 \end{aligned}$ $F$-matrix and $R$-matrix by pentagon relation and hexagon relation $\left(F_1^{111}\right)=\left[\begin{array}{cc} \tau & \sqrt{\tau} \\ \sqrt{\tau} & -\tau \end{array}\right]$ where $\tau=e^{i 2 \pi / 5}+e^{-i 2 \pi / 5}=(\sqrt{5}-1) / 2$ $R^{11}=\left(\begin{array}{cc} e^{-4 \pi i / 5} & 0 \\ 0 & e^{3 \pi i / 5} \end{array}\right)$

1.3. Example 2: Ising anyons

The Ising anyon model consists of two non-trivial particles $\psi$ (fermion) and $\sigma$ (anyon) satisfying the fusion rules

• $1 \times 1=1$
• $1 \times \psi=\psi$
• $1 \times \sigma=\sigma$
• $\psi \times \psi=1$
• $\psi \times \sigma=\sigma$
• $\sigma \times \sigma=1+\psi$

we can find a non-trivial fusion space in the same charge sector, which basis can be associated with the two fusion channels and denoted $\{|(\sigma \sigma) \sigma ; 1 \sigma ; \sigma\rangle,|(\sigma \sigma) \sigma ; \psi \sigma ; \sigma\rangle\}$ The $F$-matrix to change the basis to fusing from right to left is given by $F=F_{\sigma \sigma \sigma}^\sigma=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right)$ The $R$-matrix describing the clockwise exchange of the two left-most $\sigma$ anyons is given by $R=\left(\begin{array}{cc} R_{\sigma \sigma}^1 & 0 \\ 0 & R_{\sigma \sigma}^\psi \end{array}\right)=e^{-i \frac{\pi}{8}}\left(\begin{array}{cc} 1 & 0 \\ 0 & e^{i \frac{\pi}{2}} \end{array}\right)$

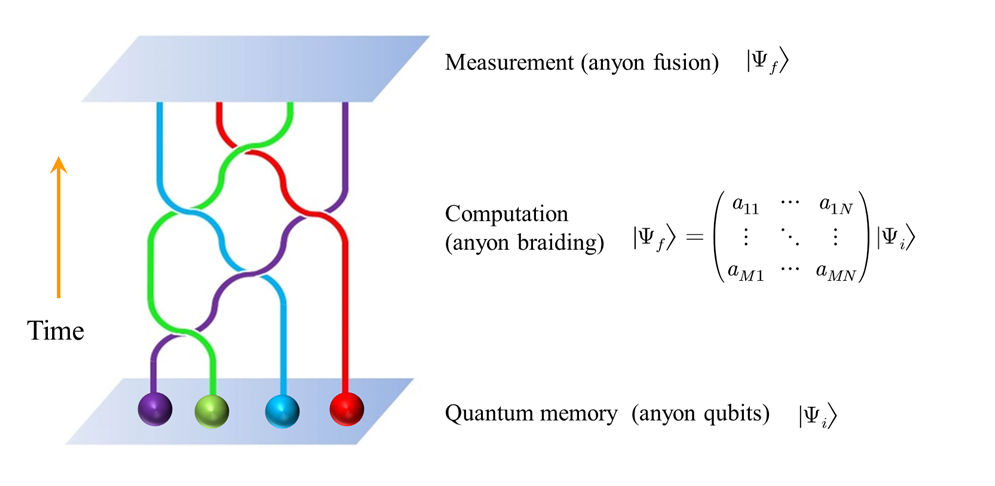
2. Quantum computation with anyons

1. Initialization of a TQC
2. Quantum gates - Braiding anyons
3. Measurements - Fusing anyons

2.1.1. Elementary braiding

two possible fusion for Fibonacci Anyon model (Two Bases)

Basis states for the two-dimensional Hilbert space (a qubit) spanned by two pairs of anyons with total topological charge 0.

The braiding matrix of neighboring anyons

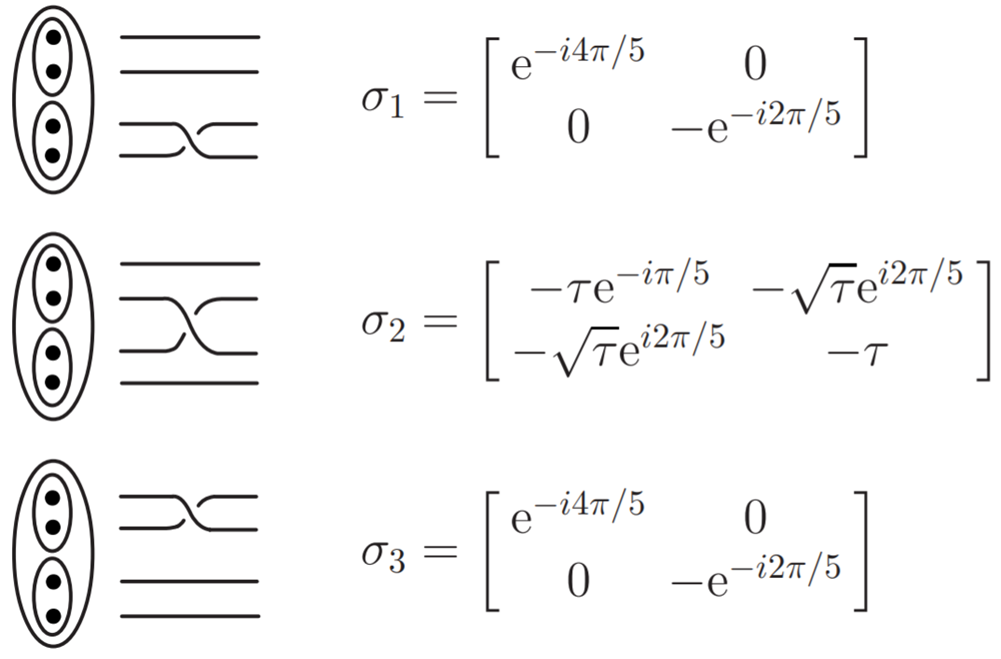
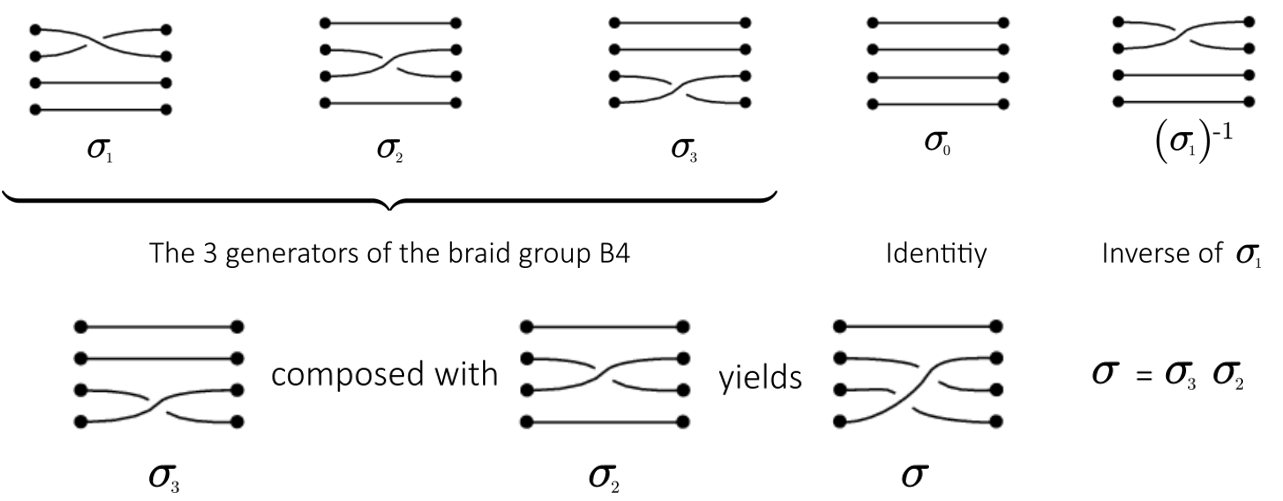
The 3 generators of the braid group $B 4$

2.1.2. Braiding to Gate

These elementary braiding can be combined to construct various quantum gates

Single-qubit gates. A generic single-qubit gate can be represented by a 2 by 2 unitary matrix $e^{i \alpha}\left[\begin{array}{cc} c c \sqrt{1-b^2} e^{-i \beta} & b e^{i \gamma} \\ -b e^{-i \gamma} & \sqrt{1-b^2} e^{i \beta} \end{array}\right]$ To search for any desired gate, we implement the brute-force algorithm [Rev. Lett. 95 , 140503 (2005)] with some modifications.

A braid with 99 anyon interchanges that approximates a phase gate, $\left|\delta_1\right|=\left|\delta_2\right|=\sqrt{1-r^2} \simeq 6.2 \times 10^{-10}$

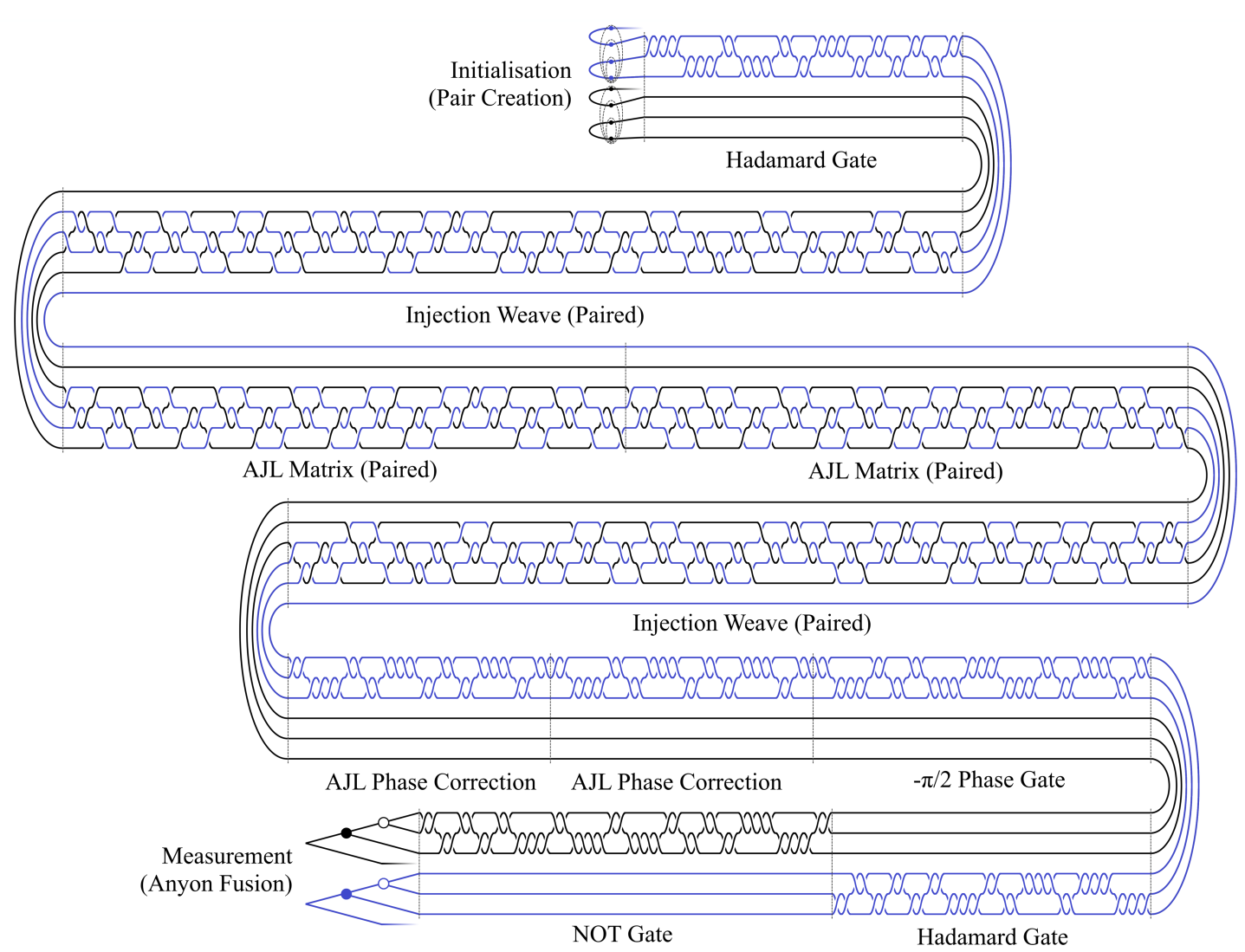
2.1.3. Braid Implementation of Algorithm

In the work Field and Simula, 2018 arXiv.1802.06176, they performed the Aharonov Jones Landau (AJL) algorithm for approximating the Jones polynomial at the complex roots of unity $\left(e^{2 \pi i / k}\right)$.

3. Appendix

3.1. Knot Invariant of the Jones polynomial