• Meet Physics
  • Topological phase matter ~ energy spectrum ~ Continuous limit
  • Interacting split-step quantum walk ~ Split step quantum walks ~ Interacting split-step quantum walk ~ Band structure ~ Phenomenology ~ Entanglement entropy

1. Meet Physics

1.1. Topological phase matter

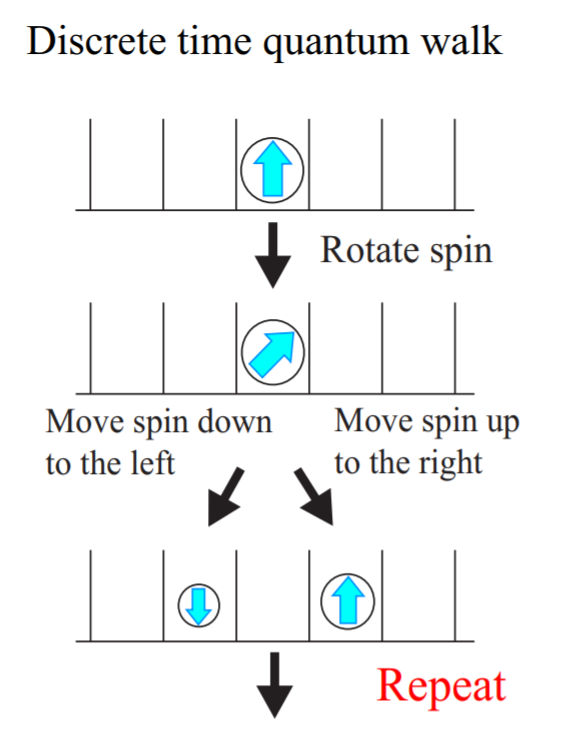
We consider a walker on a one dimensional lattice of points $x$, whose motion is determined by the orientation of its spin.

1. rotation around $y$ axis by angle $\theta$, whose operator is given by $R_{y}(\theta)=e^{-i \theta \sigma_{y} / 2} ;$
2. spin-dependent translation $T$ where spin up particle is move to the right by one lattice site and spin down particle is moved to the left by one lattice site.
3. One step of the quantum walk is given by $U=S R_{y}(\theta)$ and the evolution of the particle after many steps are studied.

A single step decomposes in:

• a spin rotation $R(\theta)= e ^{- i \sigma_{y} \theta}$,

$R_{y}(\theta)=\left(\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$

• and a shift $S=S_{\downarrow}+S_{\uparrow}$ towards the left $S_{\downarrow}$ for the spin down, and to the right $S_{\uparrow}$ for the spin up,
• the evolution operator is

$U=S[I \otimes R(\theta)] \equiv e ^{- i H_{\text {eff }}}$

where we defined an effective Hamiltonian $H_{\text {eff }}$

Using the momentum representation $\begin{aligned} S &=\sum_{j}|j+1\rangle\langle j|\otimes| \uparrow\rangle\langle\uparrow|+| j-1\rangle\langle j|\otimes| \downarrow\rangle\langle\downarrow| \\ &=\int_{-\pi}^{\pi} d k e^{i k \sigma_{z}} \otimes|k\rangle\langle k| \end{aligned}$ the effective Hamiltonian becomes diagonal $H_{ eff }=\int_{-\pi}^{\pi} d k|k\rangle\langle k| \otimes E_{\theta}(k) n _{\theta}(k) \cdot \sigma$ with the energy spectrum $\cos E_{\theta}(k)=\cos \theta \cos k$ and the spin quantization axis $n _{\theta}(k)$ of the spinor eigenstates is, $n _{\theta}(k)=\frac{1}{\sin E_{\theta}(k)}\left(\begin{array}{c} \sin \theta \sin k \\ \sin \theta \cos k \\ -\cos \theta \sin k \end{array}\right)$

energy spectrum

The dispersion relation of the rotation quantum walk $E_{\theta}(k)$, for various values of $\theta=0, \pi / 6, \pi / 2,5 \pi / 6 ;$

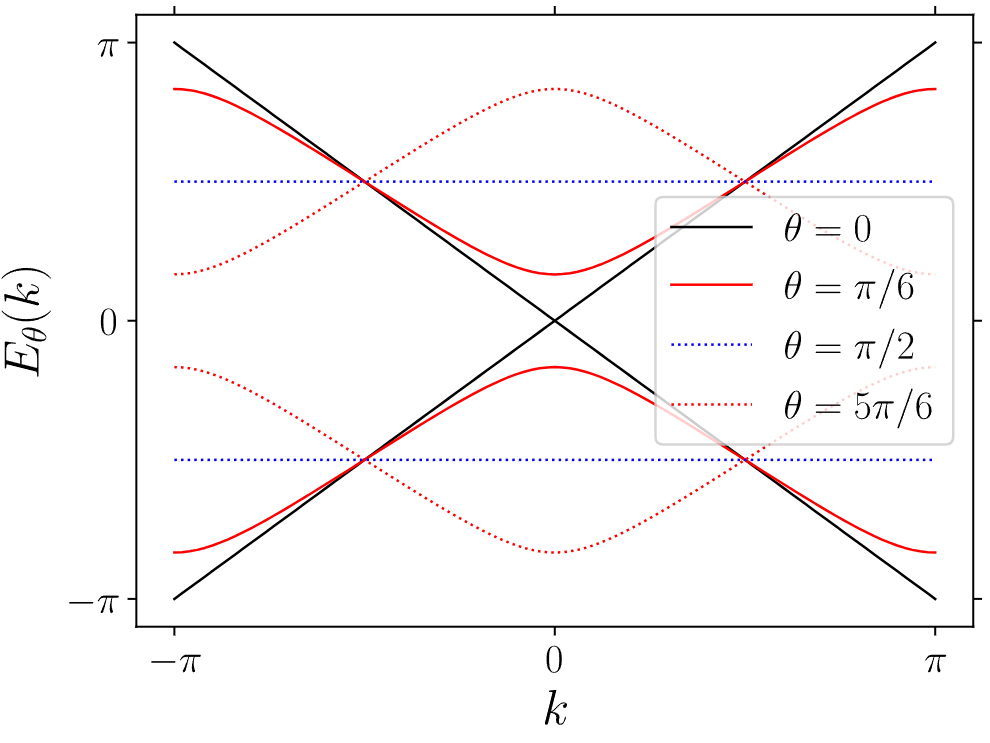
• $\theta=0$ shows a dirac point at $k=0 ;$
• $\theta=\pi / 2$ gives flat bands;
• intermediate values of $\theta$ show gapped bands.
• Observe de similarity with the polyacetylene model. Below and above the dirac point, the bands topology changes.

singularity

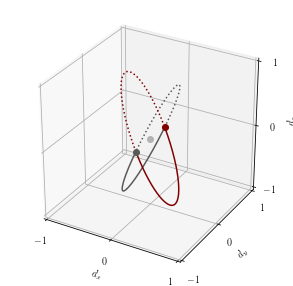
It is worth noting that at $\theta=0, \pi$ the unit vector $n$ has a singularity: numerator and denominator vanish at $k=0, \pi$. Geometrically, it corresponds to a discontinuity of the normal vector $A (\theta)$, the unit vector perpendicular to the plane of rotation defined by $n _{\theta}(k)$ when $k$ varies between $(-\pi, \pi]$ : $A (\theta)=-\operatorname{sgn}(\sin \theta)(\cos \theta, 0, \sin \theta)$ which can be obtained using, for instance, two points $k=0, \pi / 2$ on the circle, $A (\theta)=\frac{ n _{\theta}(0) \times n _{\theta}(\pi / 2)}{\left| n _{\theta}(0) \times n _{\theta}(\pi / 2)\right|}$ The vector $A$ can be used to demonstrate the existence of a chiral symmetry associated with the effective hamiltionian: $e ^{ i \pi A \cdot \sigma / 2} H e ^{- i \pi A \cdot \sigma / 2}=-H$ A change in the sigh of $\theta$ is accompanied with a chirality change: trying to put together the two walks, will create a "defect" as in the SSH model: an edge state with zero (op $\pi$ ) energy, spatially localized.

Using a python code we can investigate the behavior of the quantum walk when an interface separating two topologically different regions is introduced at $x=0$. The angle of rotation is split into two values $\theta_{-}$on the left of the origin $(x \leq 0)$ and $\theta_{+}$on the right $(x>0$.

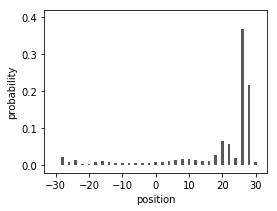
1. In the first figure the rotation angles on both sides of the interface are equal, and the normal ballistic propagation of the probability is observed.
2. In the second figure a localized edge state appears at the interface separating, on the left, $a \theta<0$ region, and, on the right, $a \theta>0$ region. One also observes the appearance of a reflected wave walking in the left direction.

Continuous limit

We investigate the low energy large wavelength behavior of the quantum walk by taking the hydrodynamic limit $E, k \rightarrow 0$. In this limit the effective hamiltonian, $H(\theta, k)=\frac{E_{\theta}(k)}{\sin E_{\theta}(k)}\left(\begin{array}{cc} -\cos \theta \sin k & - i \sin \theta e ^{ i k} \\ i \sin \theta e ^{- i k} & \cos \theta \sin k \end{array}\right)$ is given by, $H(\theta, k)=\tan \theta \sigma_{y}+\sec \theta\left(\sin \theta \sigma_{x}-\cos \theta \sigma_{z}\right) k$ (to the lowest order in $k$ ). Making now the usual subtitution, $i k \rightarrow \frac{\partial}{\partial x}$ one obtains a Dirac-like hamiltonian $H_{D}=c \alpha p+m c^{2} \beta$ with speed term, $c=\frac{1}{\cos \theta}, \quad \alpha=\cos \theta \sigma_{x}-\sin \theta \sigma_{z}$ and mass term, $m c^{2}=\tan \theta, \quad \beta=\sigma_{y}$ We approximated $\frac{E \Delta t}{\sin (E \Delta t)} \approx \frac{1}{\cos \theta}$ in order to preserve the property $| n |^{2}=1$, or equivalently, $\alpha^{2}=1, \beta^{2}=1$ where we put explicitly $\Delta t$ to show that the hydrodynamic limit is a two parameter approximation $E, k \rightarrow 0$, or $E \Delta t, k \Delta x \rightarrow 0 .$

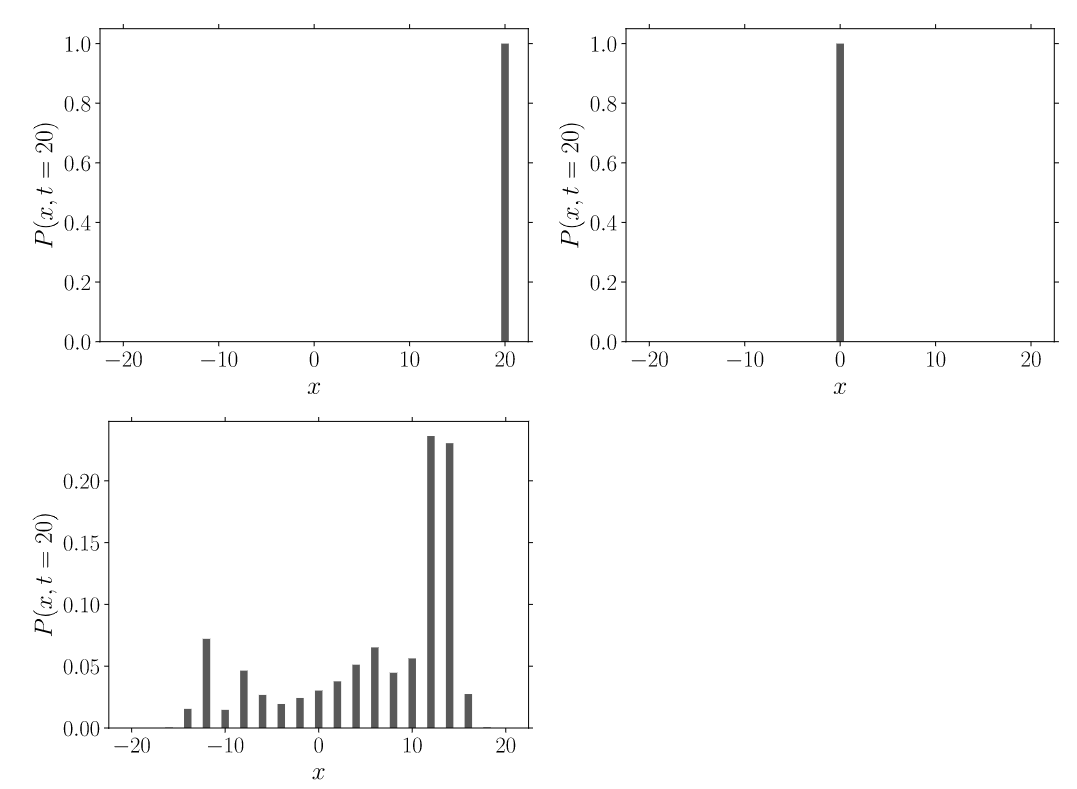
Simple quantum walk for three values of the rotation angle: $\theta=0, \pi / 2, \pi / 4 .$ The initial state has probability one at $x=0$ and spin up.

1. After 20 time steps the position probability is one at $x=20$ for $\theta=0$, corresponding to a velocity 1 and zero mass, thus the particle moves uniformly in the positive direction;
2. for $\theta=\pi / 2$, the mass and velocity become infinity, and the particle stays near its initial position. In fact, in this case the particle alternatively moves between $x=0$ and $x=1$. These results are in agreement with the prediction of the continuous limit.
3. At intermediate values of $\theta$, the distribution is more complicated $(\theta=\pi / 4)$.

1.2. Interacting split-step quantum walk

Split step quantum walks

Split-step quantum walks is a simple extension of conventional quantum walks which have one additional rotation and translation process. The complete protocol is as follows;

1. Rotation of the spin around $y$ axis by angle $\theta_{1}$, corresponding to the operation $R_{y}\left(\theta_{1}\right)=e^{-i \theta_{1} \sigma_{y} / 2}$.
2. Translation of spin up particle to the right, given by $T_{\uparrow}=\sum_{j}|j+1\rangle\langle j|\otimes| \uparrow\rangle\langle\uparrow|+ 1 \otimes| \downarrow\rangle\langle\downarrow|$. Spin down particle stays in the original position.
3. Second rotation of the spin around $y$ axis by angle $\theta_{2}$, corresponding to the operation $R_{y}\left(\theta_{2}\right)=$ $e^{-i \theta_{1} \sigma_{y} / 2} .$
4. Translation of spin down particle to the left, given by $T_{\downarrow}=\sum_{j}|j-1\rangle\langle j|\otimes| \downarrow\rangle\langle\downarrow|+ 1 \otimes| \uparrow\rangle\langle\uparrow| .$ Spin up particle stays in the original position.

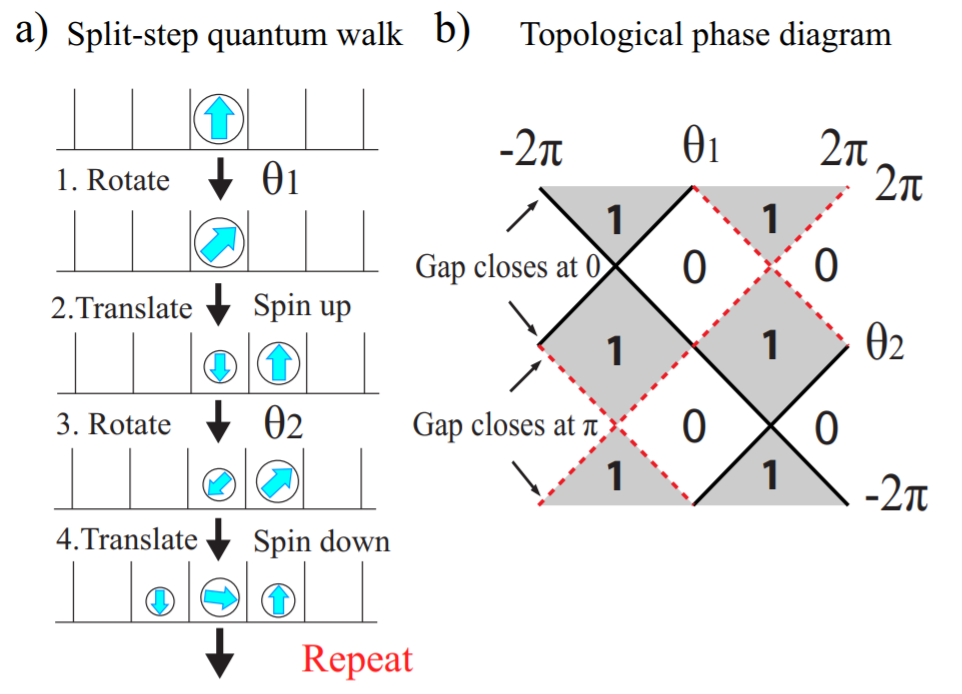
Interacting split-step quantum walk

A quantum system of two particles is defined by the set of base vectors, $\left|x_{1} s_{1}\right\rangle \otimes\left|x_{2} s_{2}\right\rangle=\left|x_{1} s_{1} x_{2} s_{2}\right\rangle$ where the indices 1 and 2 are for the particles, $x$ is the particle position and $s$ its spin. The two particles execute on the line a discrete quantum walk $U=V\left(U_{0} \otimes U_{0}\right)$, defined by the composition of the split-step operator, $U_{0}|x s\rangle=U_{0}=T R\left(\theta_{-}\right) T_{+} R\left(\theta_{+}\right)|x s\rangle$ which depends on the two angles $\theta_{\pm}$, and an interaction operator, $V\left|x_{1} s_{1} x_{2} s_{2}\right\rangle= e ^{ i \phi} \delta_{x_{1}, x_{2}}\left|x_{1} s_{1} x_{2} s_{2}\right\rangle$ which adds a phase $\phi$ to the quantum state when the two particles are at the same site. The split-step operator rotates the particle spin, $R(\theta)=1_{x} \otimes \exp \left( i \sigma_{y} \theta\right)$ and translates the spin-up projection one lattice step to the right, $T_{+}=\sum_{x}(|x+1\rangle\langle x|\otimes| 0\rangle\langle 0|+| x\rangle\langle x|\otimes| 1\rangle\langle 1|)$ and the spin-down projection one step left, $T=\sum_{x}(|x\rangle\langle x|\otimes| 0\rangle\langle 0|+| x-1\rangle\langle x|\otimes| 1\rangle\langle 1|) .$ The interaction depends on the distance of the two particles, it breaks then the translation symmetry of the free system, but preserves the conservation of center of mass motion.

One important property of the split-step quantum walk is that its energy bands structure possesses a nontrivial topology

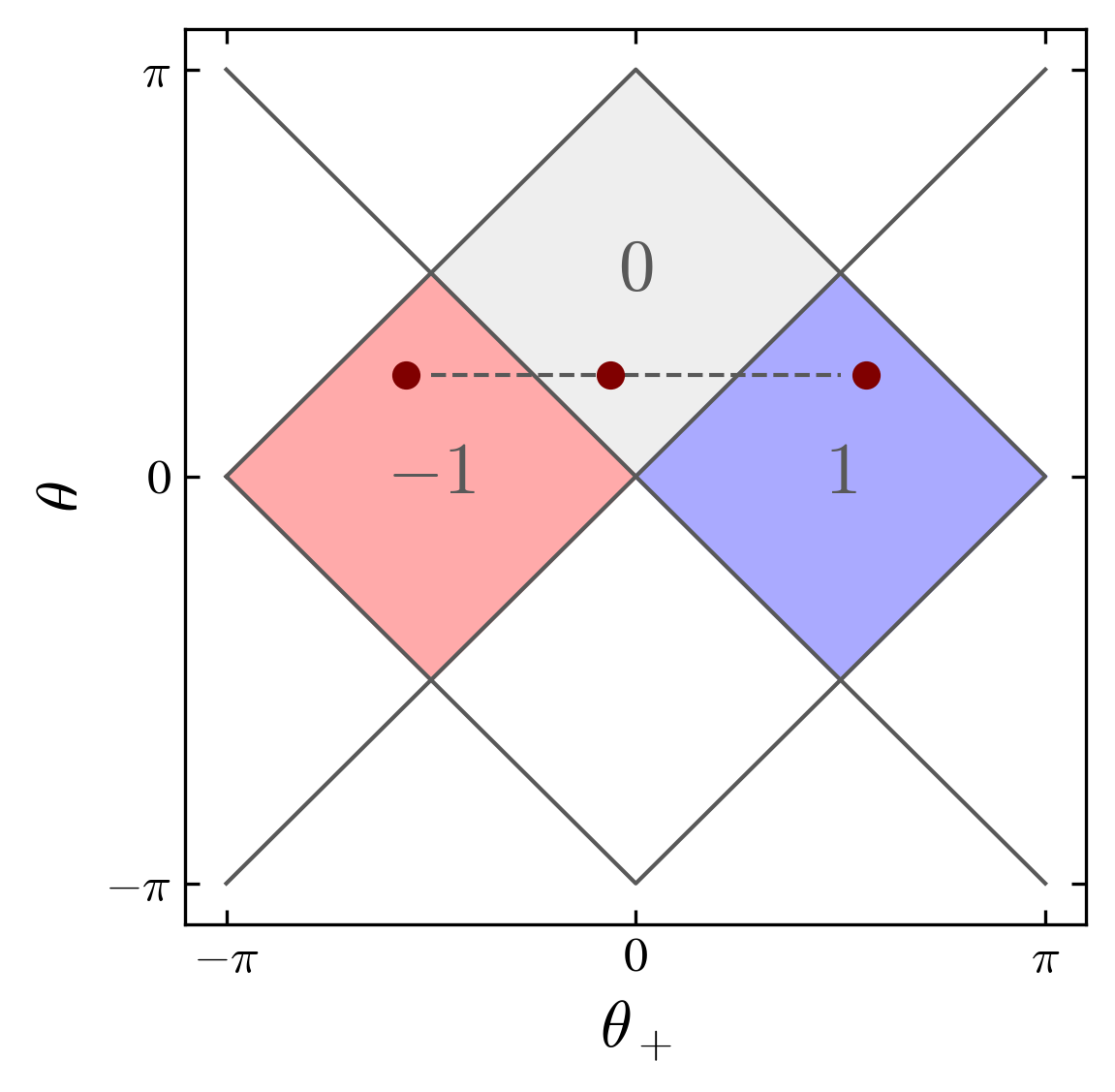
Topological charge in the plane defined by the two rotation angles.

Band structure

We compute the spectrum of the one step operator $U$, $U\left|E_{n}\right\rangle=E_{n}\left|E_{n}\right\rangle$ by exact diagonalization, for the homogeneous (one phase) system. For the non interacting case, we find a gapped spectrum. This structure is preserved for the interacting case with however the appearance of bound modes within the gaps (figure).

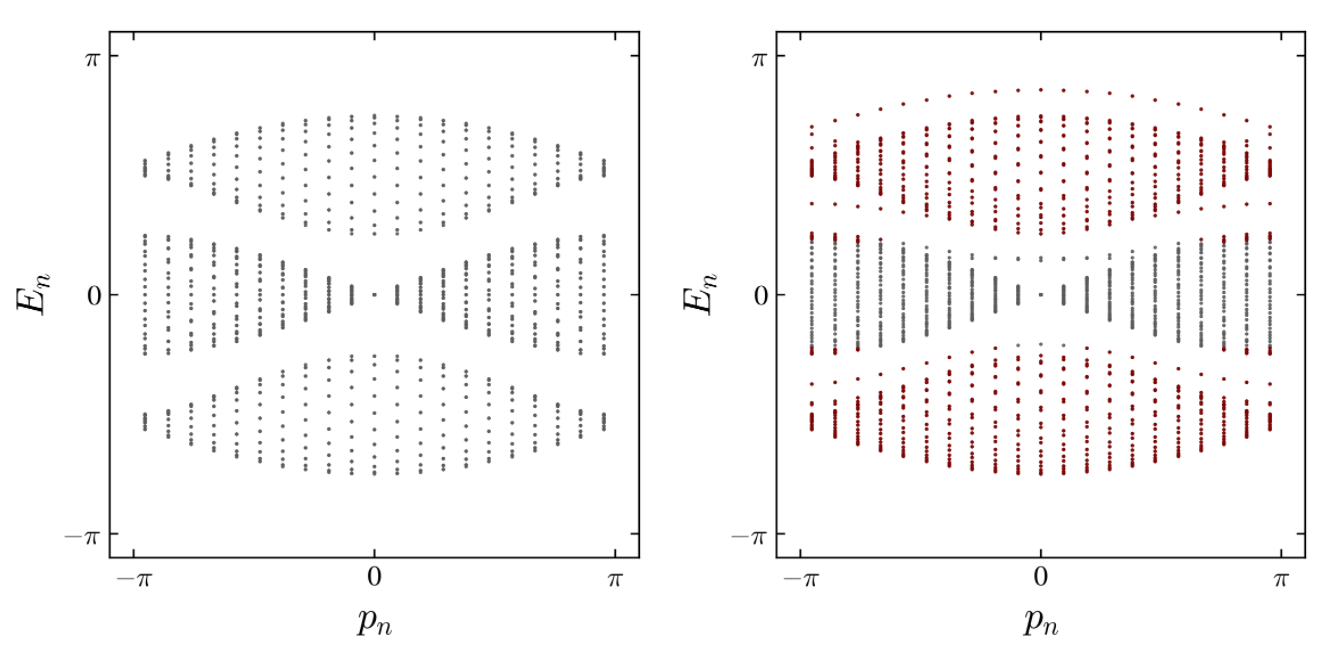
Energy bands for the non interacting case $\phi=0$ and interacting case $\phi=\pi / 3 .$ Note the appearance of bound states within the gap, in the intearcting case. The quasienergies are ordered by the value of the momentum of the center of mass of the two particles $p_{n}$. The bounded state corresponds to the binding of the two particles in a "molecular" state

Phenomenology

We investigate the evolution of the two particle probability P(t)P(t) (images above):

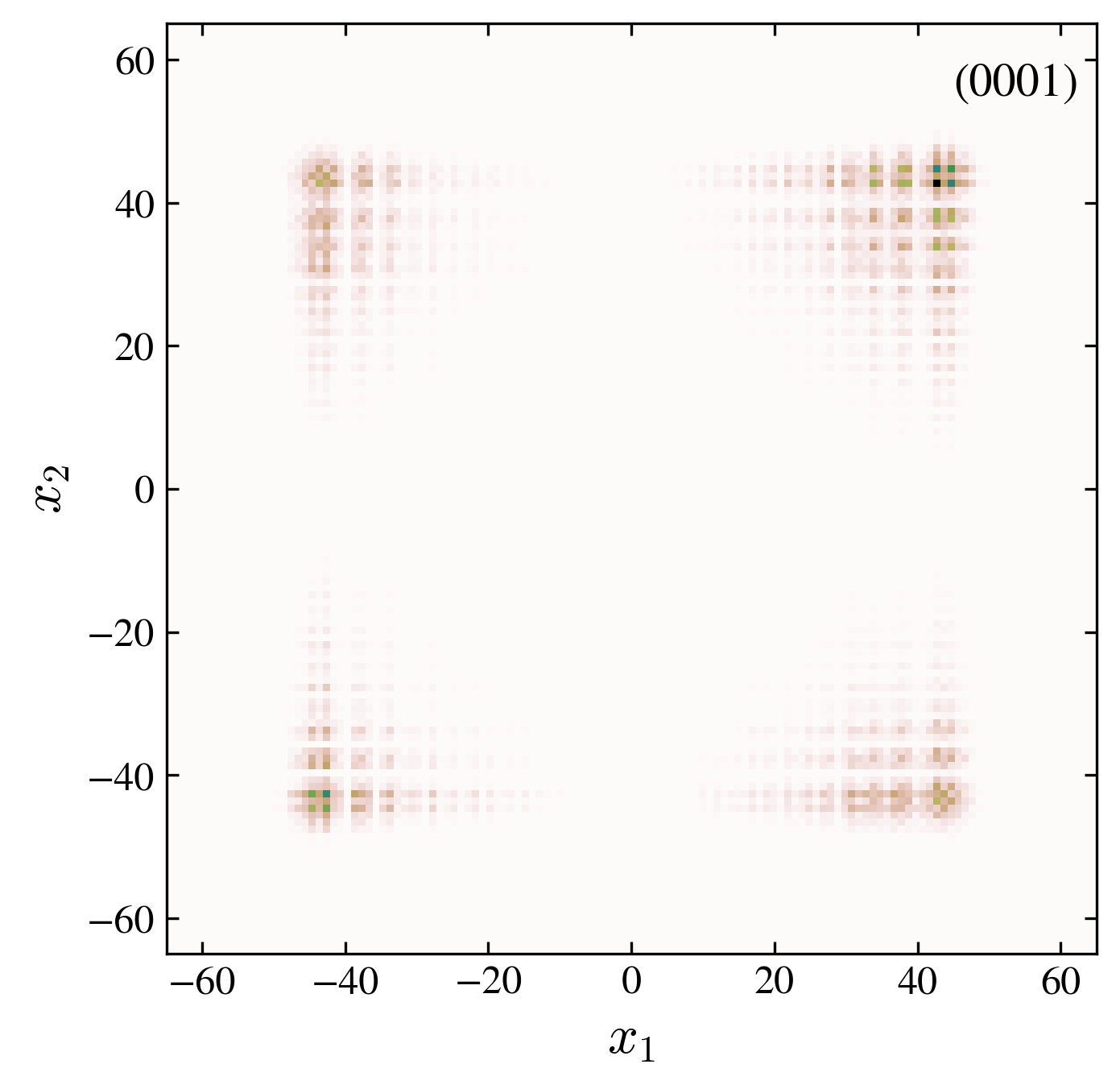
• “0001” free trivial case (there is no interaction or interface): the two particles spread together ballistically. This case follows the one particle quantum walk, without edge state.

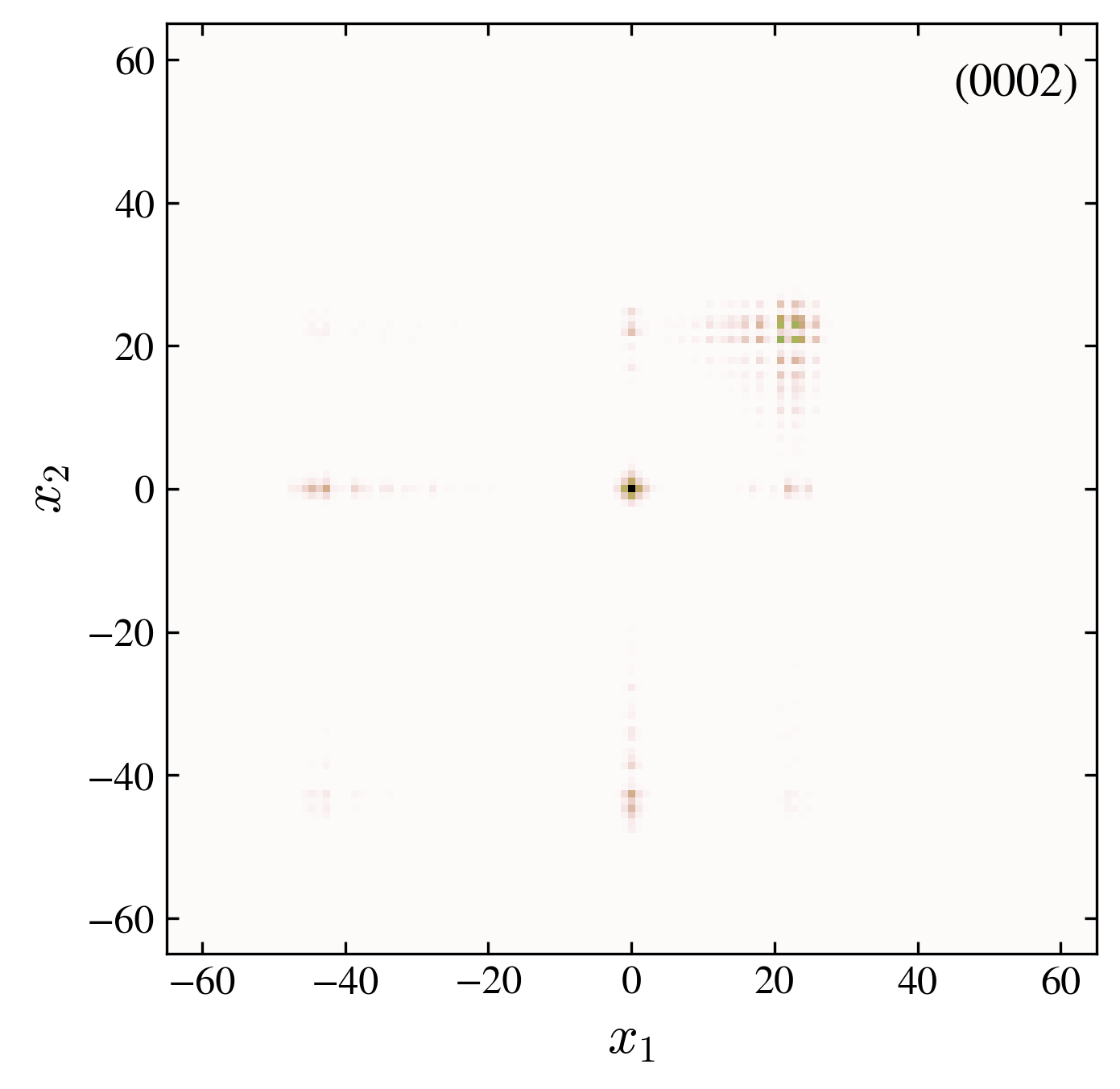
• “0002” free, 01-interface: the presence of a localized state contributes to a finite probability P(t)P(t) to find the two particles at the origin at long times.

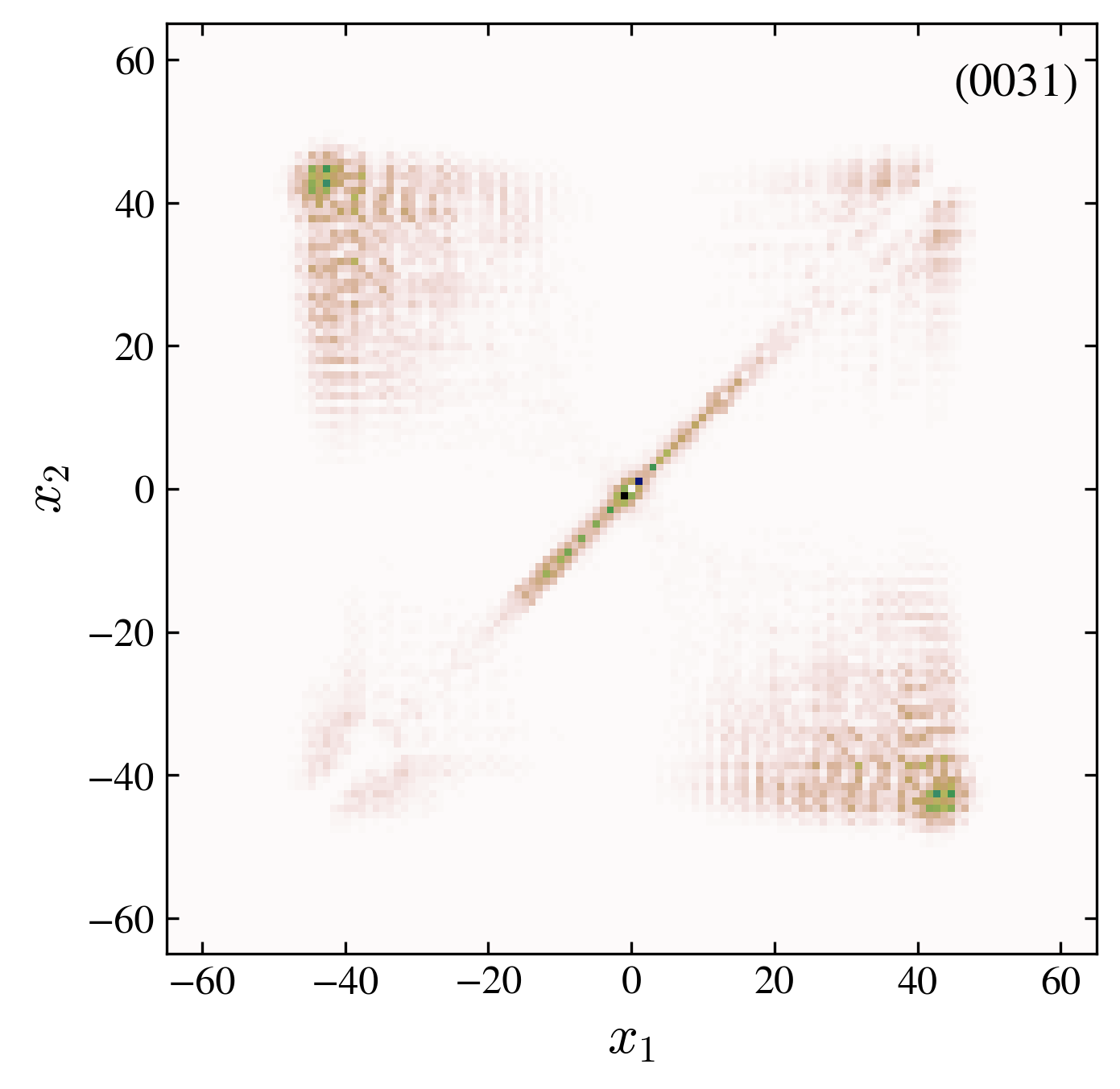
• “0031” interaction, trivial: in a trivial topology, the interaction allows a binding of the two particles. In addition a localized state appears at the origin.

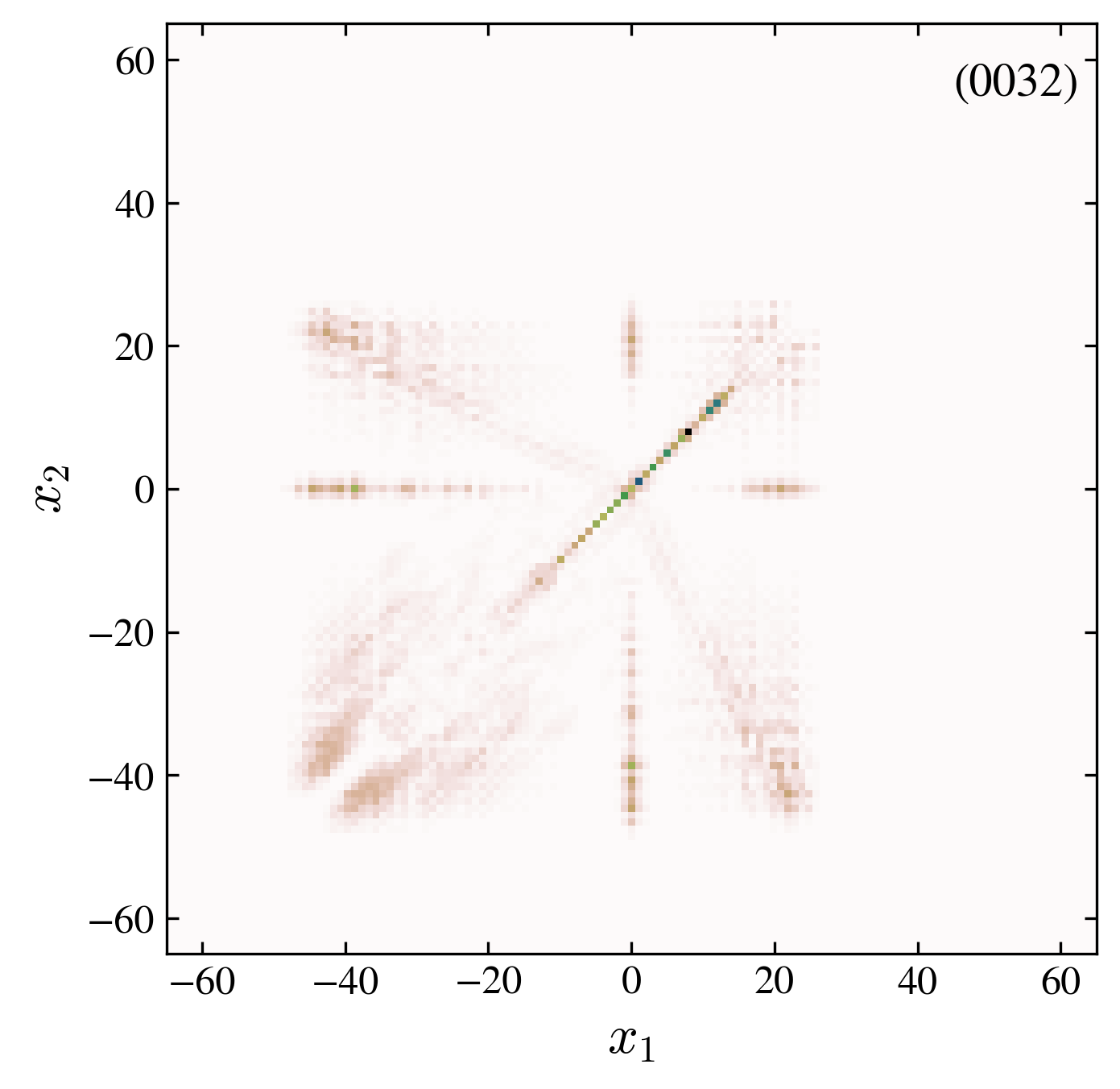
• “0032” interaction, 01-interface: the addition of the edge state suppress the antisymmetric spreading, observed in the “0031” case.

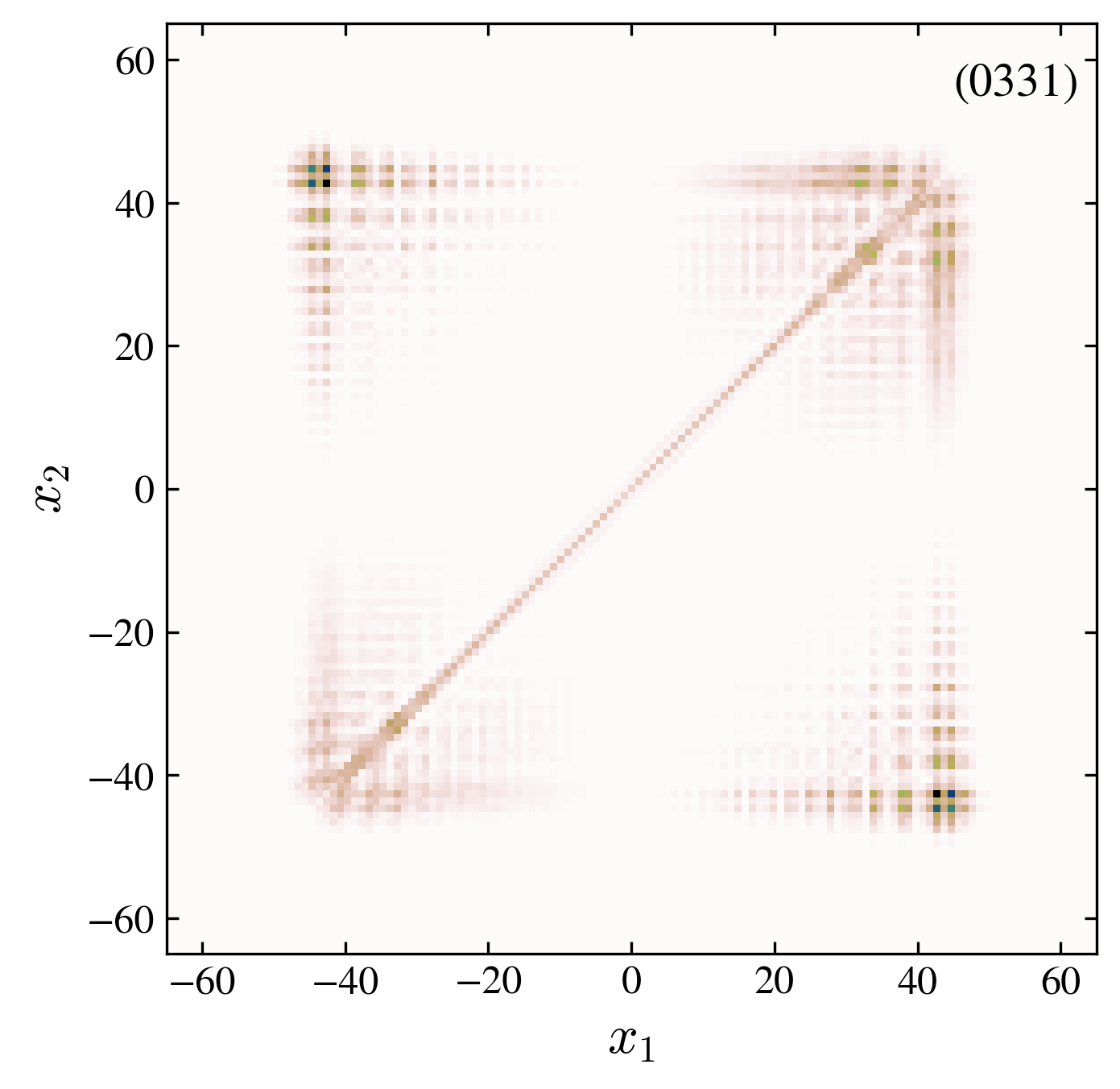
• “0331” interaction, trivial, antisymmetric: with an antisymmetric initial state the localization at the origin, present in the symmetric case “0031”, vanishes. However, in spite of the tendency of the two particles to avoid each other, a binding state is present.

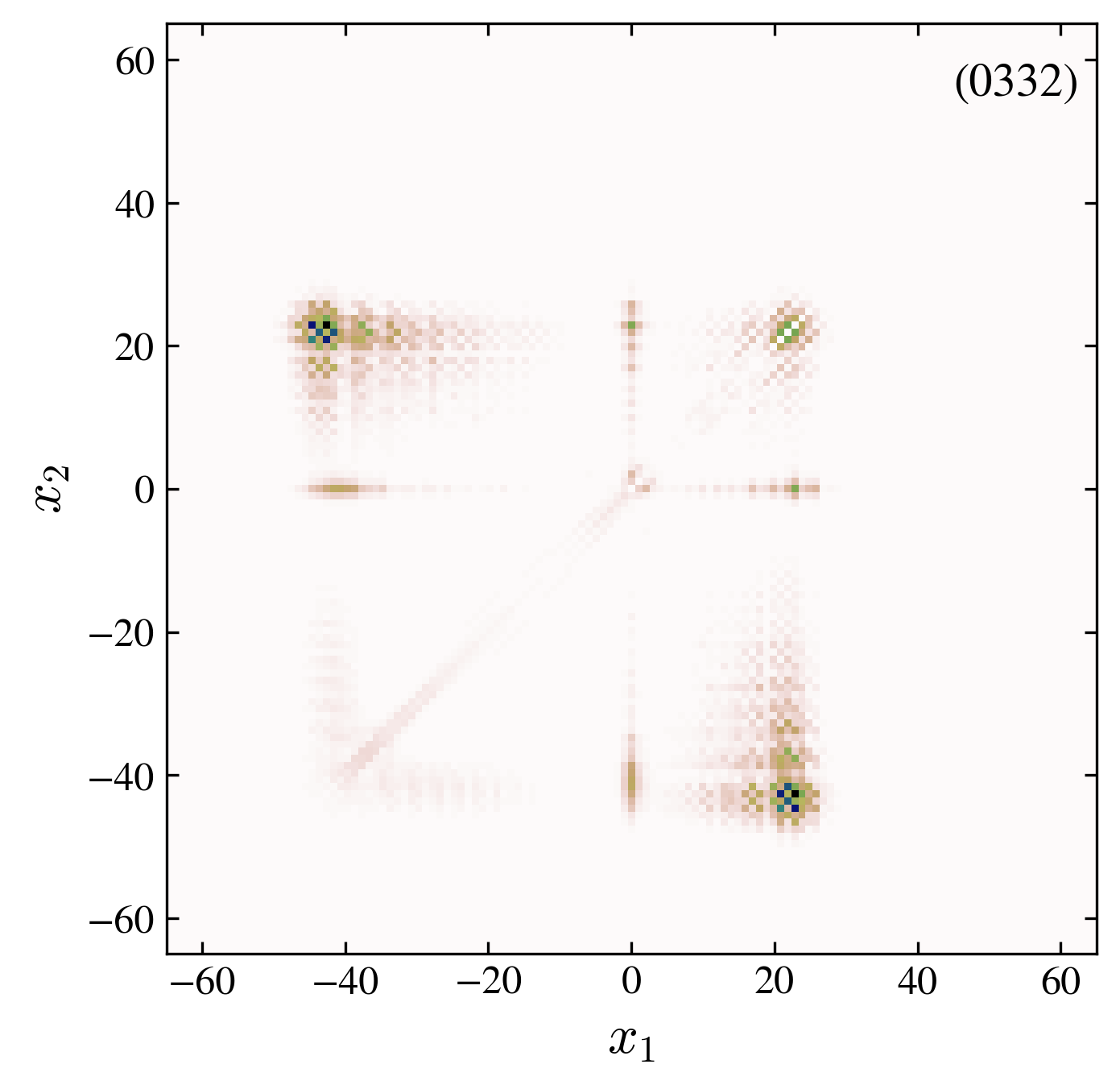
• “0332” interaction, 01-interface, antisymmetric: the interaction suppress the localized state and modifies the velocity of propagation of the probability.

Entanglement entropy

The existence of localized states has a profound impact on the behavior of the entanglement entropy: $S_{x}(t)=-\operatorname{Tr} \rho_{x}(t) \log \rho_{x}(t), \rho_{x}(t)=\operatorname{Tr}_{\bar{x}} \rho_{x, \bar{x}}(t)$

• Indeed, in the delocalized state it grows logarithmically,

$S_{x}(t) \sim \alpha \log t,$

• while in the localized case its growth is very slow, as an iterated logarithm,

$S_{x}(t) \sim \log (\xi \log t)$

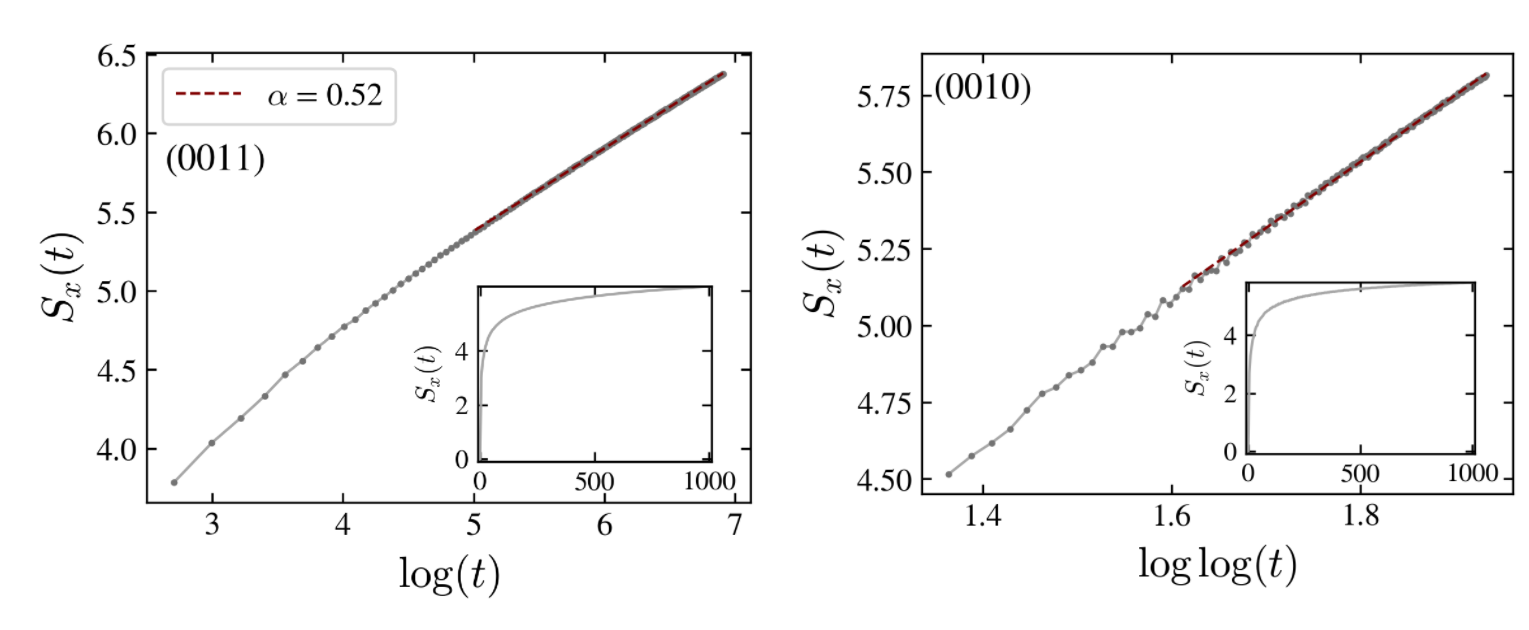
Entanglement entropy for the delocalized and localized cases: a transition between logharithmic and double logarithmic growth is observed.