Adiabatic quantum computation

• Theorem
  • The adiabatic theorem
    • Proof
  • Adiabatic quantum computation
  • Universality
  • Quantum Annealing
    • Example
• Applications
  • Transverse Ising model
  • One Qubit Examples
  • Adiabatic Grover ~ Quadratic speedup

Reference

1. Dr Steven Herbert, Quantum Computing (CST Part II) Lecture 15: Adiabatic Quantum Computing
2. Andrew Childs's presentation: Overview of adiabatic quantum computation
3. Andrew M. Childs: Lecture Notes on Quantum Algorithms
4. Advanced Quantum Algorithms Lecture by Giulia Ferrini, Anton Frisk Kockum, Laura García-Álvarez, Pontus Vikstål (2020)
5. [Rev. Mod. Phys. 90, 015002] Albash and Lidar, 2018
6. Scott Pakin, Quantum Annealing, NSF/DOE Quantum Science Summer School, 8 June 2017

1. Theorem

1. The adiabatic theorem
2. Adiabatic quantum computation
3. Universal quantum computing
4. Quantum Annealing

1.1. The adiabatic theorem

Adiabatic quantum computation is based on the adiabatic theorem.

A physical system remains in its instantaneous eigenstate if a given perturbation is acting on it slowly enough and if there is a gap between the eigenvalue and the rest of the Hamiltonian's spectrum

—— The adiabatic theorem. (1928) by Max Born and Vladimir Fock

More mathematically,

If we have a time-varying Hamiltonian, $\mathrm{H}(t)$, which is initially $\mathrm{H}_I$ at $t=0$, and subsequently $\mathrm{H}_F$ at some later time, $t=t_F$, then if the system is initially in the ground-state of $\mathrm{H}_I$, and as long as the time-evolution of the Hamiltonian is sufficiently slow, the state is likely to remain in the ground-state throughout the evolution, therefore being in the ground-state of $\mathrm{H}_F$ at $t=t_F$.

In other words, if a quantum system starts in a ground-state, so long as we evolve the state slowly, it is likely to remain in a ground-state.

1.1.1. Proof

What exactly is a "slowly evolving state"? The proof of quantum adiabatic theorem is complex. It suffices to simply know the existence of the quantum adiabatic theorem. If you are interested in the proof, please refer to the following literature:

1. Andrew Childs' lecture notes, Chapter 27 The quantum adiabatic theorem
2. Advanced Quantum Algorithms, Chapter 7 Adiabatic quantum computation, Giulia Ferrini, Anton Frisk Kockum, Laura García-Álvarez, Pontus Vikstål

1.2. Adiabatic quantum computation

Basic strategy:

• Design a Hamiltonian $\mathrm{H}_F$ whose ground state encodes the solution of an optimization problem. $\mathrm{H}_F$ is also called final Hamiltonian.
• Prepare the known ground state of a simple Hamiltonian, $\mathrm{H}_I$, whose ground-state is easy to construct. $\mathrm{H}_I$ is also called initial Hamiltonian.
• An adiabatic evolution path, $s(t)$, which defines the Hamiltonian evolution
  • where $s(0)=1$
  • and $s\left(t_F\right)=0$

The AQC Hamiltonian can be written as $\mathrm{H}(t)=s(t) \mathrm{H}_I+(1-s(t)) \mathrm{H}_F$ For example, the linear path $s(t)=\left(1-\frac{t}{t_F}\right)$ $\mathrm{H}(t)=\left(1-\frac{t}{t_F}\right) \mathrm{H}_I+\frac{t}{t_F} \mathrm{H}_F$ Where

• when $t=0$ such that $\mathrm{H}(0)=\mathrm{H}_I$
• when $t=0$ such that $\mathrm{H}\left(t_F\right)=\mathrm{H}_F$

1.3. Universality

Adiabatic quantum computation models proved to be universal quantum computing. Which means that adiabatic quantum computing is polynomially equivalent to gate-based quantum computing.

Definition 3 (Universal Adiabatic Quantum Computation).

A time-dependent Hamiltonian $H(t), t \in\left[0, t_f\right]$, is universal for $A Q C$ if, given an arbitrary quantum circuit $U$ operating on an arbitrary initial state $|\psi\rangle$ of $n p$-state particles and having depth $L$, the ground state of $H\left(t_f\right)$ is equal to $U|\psi\rangle$ with probability greater than $\epsilon>0$, the number of particles $H(t)$ operates on is poly $(n) \forall t$, and $t_f=\operatorname{poly}(n, L)$.

The proofs for these statements can be found in following reference if you are interested

• Technical details for the proof of the universality of $A Q C$ using the History State construction.

  • Ref. [Rev. Mod. Phys. 90, 015002, Albash and Lidar, 2018] .Appendix C

• The AQC can efficiently simulate the circuit model

  • Aharonov, Dorit, et al. "Adiabatic quantum computation is equivalent to standard quantum computation." SIAM review 50.4 (2008): 755-787.

• The circuit model can efficiently simulate the AQC is relatively straight forward

  • Farhi, Edward, et al. "Quantum computation by adiabatic evolution." arXiv preprint quant-ph/0001106 (2000).

1.4. Quantum Annealing

Adiabatic quantum computation shares a close relationship with quantum annealing (QA). Quantum annealing also encodes the solution to a problem in the ground state of some final Hamiltonian.

quantum annealing definition by [Hauke et al., 2020]

Quantum Annealing (QA) is a heuristic quantum algorithm that is based on the Adiabatic Quantum Computation model. It aims at solving hard combinatorial optimization problems, by using an Ising Hamiltonian as the target Hamiltonian.

The solution of the desired combinatorial optimization problem encoded in the ground state of an Ising Hamiltonian. A quantum annealing (QA) process finds the solution by converting an initial Hamiltonian to the Ising Hamiltonian. Thus, quantum annealing can be thought of as optimization problems restricted to adiabatic quantum computations. Due to this, a less general Hamiltonian is sufficient for quantum annealing compared to adiabatic quantum computation.

Basic strategy of Quantum annealing:

1. Design a Hamiltonian $\mathrm{H}_F$ whose ground state encodes the solution of an optimization problem. $\mathrm{H}_F$ is also called final Hamiltonian.
2. A transverse field Hamiltonian, $\mathrm{H}_D$, which does not commute with $\mathrm{H}_F$.
3. Starting in an arbitrary initial state, we evolve a system according to the evolution Hamiltonian

$\mathrm{H}(t)=\mathrm{H}_F+\Gamma(t) \mathrm{H}_D$ where

• $\Gamma(t)$ is the transverse field coefficient, which is initially very high, and reduces to zero over time.

Distinctions between AQC and QA

1.4.1. Example

Problem Hamiltonian
$\mathcal{H}_P=-\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1} J_{i, j} \sigma_i^Z \sigma_j^Z-\sum_{i=0}^{N-1} h_i \sigma_i^Z$ where

• Longitudinal interactions $-\sum_{i=0}^{N-2} \sum_{j=i+1}^{N-1} J_{i, j} \sigma_i^Z \sigma_j^Z$
• Longitudinal field $-\sum_{i=0}^{N-1} h_i \sigma_i^Z$

Goal (what the hardware does)

• Minimize $\sigma_i \in\{-1,+1\}$ subject to provided $J_{i, j} \in \mathbb{R}$ and $h_i \in \mathbb{R}$ coefficients
• In other words, a quantum optimization program is merely a list of $J_{i, j}$ and $h_i$

Adding a time-dependent transverse field: $\begin{aligned} \mathcal{H}_S(s)=&\frac{\varepsilon(s)}{2} \mathcal{H}_P-\frac{\Delta(s)}{2} \sum_{i=0}^{N-1} \sigma_i^x \\ =&\frac{\varepsilon(s)}{2}\left(\sum_{\langle i, j\rangle} J_{i, j} \sigma_i^Z \sigma_j^Z+\sum_{\langle i\rangle} h_i \sigma_i^Z\right)-\frac{\Delta(s)}{2} \sum_{\langle i\rangle} h_i \sigma_i^x \end{aligned}$ Where

• The programmer specifies the $J_{i, j}$ and $h_i$, and the system solves for the $\sigma_i^Z$
• $\sigma_i^Z \in\{-1,+1\}$
• Nominally, $J_{i, j} \in \mathbb{R}$ and $h_i \in \mathbb{R}$, but the hardware limits these to a small set of distinguishable values in the ranges $J_{i, j} \in[-1,+1]$ and $h_i \in[-2,+2]$
• Programmer specifies the total annealing time, $T \in[5,2000] \mu \mathrm{s}$
• $s=t / T$ (i.e., time normalized to $[0,1])$
• $\varepsilon(s)$ and $\Delta(s)$ are scaling parameters (not previously user-controllable but most recent hardware provides a modicum of control over the shape)

2. Applications

1. Transverse Ising model
2. One Qubit Examples
3. Adiabatic Grover

2.1. Transverse Ising model

The initial Hamiltonian in transverse Ising model is $H_B=-\sum_{j=1}^n \sigma_x^{(j)}$ with the known ground state $\begin{aligned} |s\rangle &=|+\cdots+\rangle \\ &=\sum_{z \in\{0,1\}^n}|z\rangle \end{aligned}$ The final Hamiltonian (or problem Hamiltonian) in transverse Ising model is $H_P=\sum_{j \in \mathbb{Z}_n} \frac{1}{2}\left(1-\sigma_z^{(j)} \sigma_z^{(j+1)}\right)$ therefore, the total Hamiltonian is $\tilde{H}(s)=(1-s) H_B+s H_P$ Diagonalize by fermionization (Jordan-Wigner transformation)

Result: $\Delta \propto \frac{1}{n}$ (at critical point of quantum phase transition) $\begin{aligned} &\left|E_0(s \approx 0)\right\rangle \approx|+\cdots+\rangle \\ &\left|E_0(s \approx 1)\right\rangle \approx \frac{1}{\sqrt{2}}(|0 \cdots 0\rangle+|1 \cdots 1\rangle) \end{aligned}$

2.2. One Qubit Examples

Consider a one-bit problem where the single clause is satisfied if and only if $z_1=1$. The problem Hamiltonian (final Hamiltonian) $H_{\mathrm{P}}=\frac{1}{2}+\frac{1}{2} \sigma_z^{(1)}$ which has $\left|z_1=1\right\rangle$ as its ground state. For the initial Hamiltonian we take $H_{\mathrm{B}}=H_{\mathrm{B}}^{(1)}=\frac{1}{2}-\frac{1}{2} \sigma_x^{(1)} .$ The interpolating Hamiltonian $\widetilde{H}(s)$ $\tilde{H}(s)=(1-s) H_{\mathrm{B}}+s H_{\mathrm{P}}$ has eigenvalues $E=\frac{1}{2}\left(1 \pm \sqrt{1-2 s+2 s^2}\right)$ which are plotted in Figure

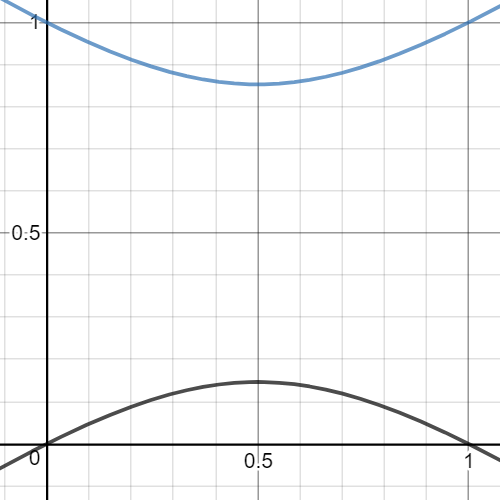
We see that Minimum gap $g_{\min }$ is not small and we could adiabatically evolve from $\left|x_1=0\right\rangle$ to $\left|z_1=1\right\rangle$ with a modest value of $T$.

At this point we can illustrate why we picked the beginning Hamiltonian, $H_{\mathrm{B}}$, to be diagonal in a basis that is not the basis that diagonalizes the final problem Hamiltonian $H_{\mathrm{P}}$. Suppose we replace $H_{\mathrm{B}}$ by $H_{\mathrm{B}}^{\prime}$ $H_{\mathrm{B}}^{\prime}=\frac{1}{2}-\frac{1}{2} \sigma_z^{(1)}$ keeping $H_{\mathrm{P}}$ as in (3.1). Now $\widetilde{H}(s)$ is diagonal in the $z$-basis for all values of $s$. The two eigenvalues are $s$ and $(1-s)$, which are plotted in Fig. 2. The levels cross so $g_{\min }$ is zero. In fact there is a symmetry, $\widetilde{H}(s)$ commutes with $\sigma_z$ for all $s$, so the appearance of the level cross is not surprising. Adiabatically evolving, starting at $\left|z_1=0\right\rangle$, we would end up at $\left|z_1=0\right\rangle$, which is not the ground state of $H_{\mathrm{P}}$. However, if we add to $H_{\mathrm{B}}$ any small term that is not diagonal in the $z$ basis, we break the symmetry, and $\widetilde{H}(s)$ will have a nonzero gap for all $s$. For example, the Hamiltonian $\left[\begin{array}{cc} s & \varepsilon(1-s) \\ \varepsilon(1-s) & 1-s \end{array}\right]$ has $g_{\min }=\varepsilon$ for $\varepsilon$ small and the eigenvalues are plotted in Fig. 3 for a small value of $\varepsilon$. This "level repulsion" is typically seen in more complicated systems whereas level crossing is not.

2.3. Adiabatic Grover

Recall the oracular problem that Grover algorithm solve:

informally the objective is to find the marked item (or possibly multiple marked items) in an unsorted database of $N$ items by accessing the database as few times as possible. More formally, one is allowed to call a function $f:\{0,1\}^n \mapsto\{0,1\}$ (where $N=2^n$ is the number of bit strings) with the promise that $f(m)=1$ and $f(x)=0$ $\forall x \neq m$, and the goal is to find the unknown index $m$ in the smallest number of calls.

The adiabatic Grover algorithm (Roland and Cerf, 2002) is the corresponding version of Grover algorithm in adiabatic quantum computing. It is perhaps the best example of a provable quantum speedup using AQC.

The initial Hamiltonian $H_0=\mathbb{1}-|\phi\rangle\langle\phi|$ where

• $|\phi\rangle$ is the uniform superposition state, $|\phi\rangle=\frac{1}{\sqrt{N}} \sum_{i=0}^{N-1}|i\rangle=|+\rangle^{\otimes n}$
• where $|\pm\rangle=\frac{1}{\sqrt{2}}(|0\rangle \pm|1\rangle)$.

The final Hamiltonian $H_1=\mathbb{1}-|m\rangle\langle m|$ where

• $|m\rangle$ is the marked state associated with the marked item.

The time-dependent Hamiltonian to be an interpolation: $\begin{aligned} H(s) &=[1-A(s)] H_0+A(s) H_1 \\ &=[1-A(s)](\mathbb{1}-|\phi\rangle\langle\phi|)+A(s)(\mathbb{1}-|m\rangle\langle m|) \end{aligned}$

1. The initial state is initialized in the ground state of $H(0)$, that is., $|\psi(0)\rangle=|\phi\rangle$

2. The evolution of the system is restricted to a two-dimensional subspace, defined by the span of

   • $|m\rangle$

   • $\left|m^{\perp}\right\rangle=\frac{1}{\sqrt{N-1}} \sum_{i \neq m}^{N-1}|i\rangle$.

In this two-dimensional subspace $H(s)$ can be written as: $[H(s)]_{|m\rangle,\left|m^{\perp}\right\rangle}=\frac{1}{2} \mathbb{1}_{2 \times 2}-\frac{\Delta(s)}{2}\left(\begin{array}{cc} \cos \theta(s) & \sin \theta(s) \\ \sin \theta(s) & -\cos \theta(s) \end{array}\right)$ where

• $\Delta(s)=\sqrt{(1-2 s)^2+\frac{4}{N} s(1-s)}$
• $\cos \theta(s)=\frac{1}{\Delta(s)}\left[1-2(1-s)\left(1-\frac{1}{N}\right)\right]$
• $\sin \theta(s)=\frac{2}{\Delta(s)}(1-s) \frac{1}{\sqrt{N}} \sqrt{1-\frac{1}{N}}$

The eigenvalues in this subspace $\begin{aligned} \varepsilon_0(s)=&\frac{1}{2}(1-\Delta(s))\\ \varepsilon_1(s)=&\frac{1}{2}(1+\Delta(s)) \end{aligned}$ The eigenvectors in this subspace $\begin{aligned} &\left|\varepsilon_0(s)\right\rangle=\cos \frac{\theta(s)}{2}|m\rangle+\sin \frac{\theta(s)}{2}\left|m^{\perp}\right\rangle \\ &\left|\varepsilon_1(s)\right\rangle=-\sin \frac{\theta(s)}{2}|m\rangle+\cos \frac{\theta(s)}{2}\left|m^{\perp}\right\rangle \end{aligned}$

Quadratic speedup

The minimum gap occurs at $s=1 / 2$ and scales exponentially with $n$ : $\Delta_{\min }=\Delta(s=1 / 2)=\frac{1}{\sqrt{N}}=2^{-n / 2}$ The adiabatic condition $\begin{aligned} \frac{\left|\left\langle\frac{d H}{d t}\right\rangle_{1,0}\right|}{g_{\min }^2} \leq \varepsilon \end{aligned}$ the asymptotic expressions are for $N \gg 1$ are proof to be $t_f \gg 2 \pi \sqrt{N}[1+\log (2 N)],$ which is a sufficient condition for the smallness of the adiabatic error, and nearly recovers the quadratic speedup expected from Grover's algorithm.